Home

Learning Hub

Articles

Types of Trees in Data Structure – A Deep Dive

The tree is another hierarchical data structure that simulates the tree structure. They include nodes where edges link them closely and are widely used in graphic display of relationships such as the genealogy tree or organizational chart. The tree’s fundamental feature is that there is a single initial node on top, and each node in turn has no or many child nodes; however, there are no loops.

What is Tree Data Structure?

Tree is a hierarchical structure, created by nodes and edges that show relations between them. This is used in computer science to increase the data storage efficiency and for purposes of categorization. It shares a lot of features with the tree that grows from the root and develops branches of child nodes. This article explained to you different types of tree data structures.

Types of Trees in Data Structure According to the Number of Children

There are many types of Tree data structures. Let’s discuss each one individually.

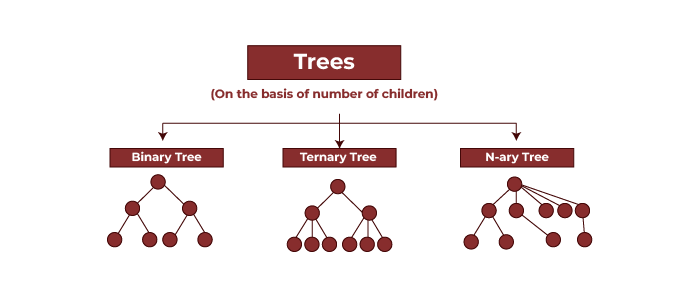
Binary Tree

Binary tree is one of the simplest forms of tree database system. Here, a node in the binary tree can have a left child, and right child at most though it can have only one of them. Due to the structure of the binary tree search or sort operation can quickly solve it.

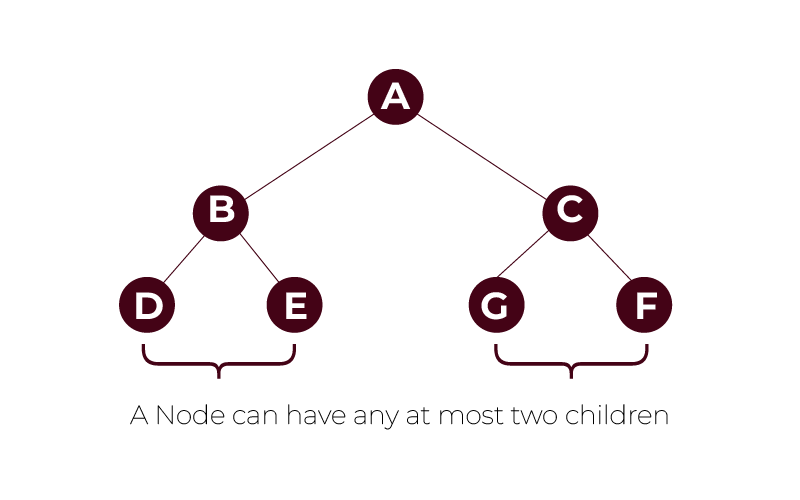
Types of Binary Tree

The basis of children binary has two types.

• Full Binary Tree: All the internal nodes of a full binary tree have two or no child nodes.

• Degenerate Binary Tree: Every internal node of the degenerate binary has just one child.

The binary tree can be divided into three types based on completion levels.

• Perfect Binary Tree: A Binary tree with all internal nodes having exactly two children and all the leaves in the same level are known as Perfect Binary Tree. In other words, From top to bottom, it comes under the fill.

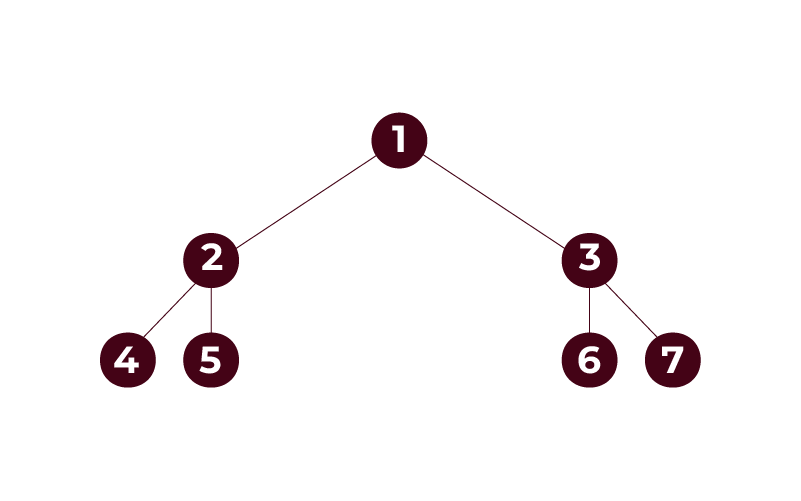
• Complete Binary Tree: A full binary tree is a certain kind of binary tree in which all the nodes are filled up to the maximum level of the tree but maybe filled only to the penultimate level in the extreme case. In simple words, The node present at a certain level all nodes of that level must be present if the last level contains nodes it can contain only nodes on the left side.

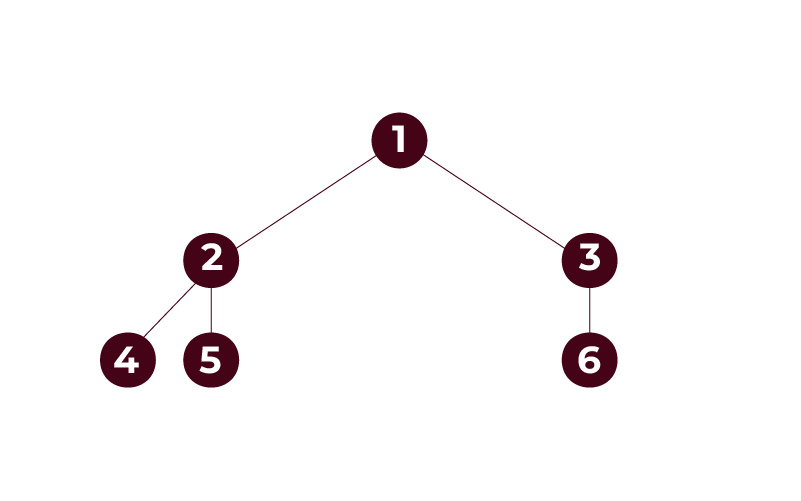
• Balanced Binary Tree:  A binary tree is one in which the heights of the left and right subtrees of any node have a maximum difference of one.  The balance condition is aimed at ensuring that the tree has moderate heights thus the easy and efficient running of operations such as insertions, deletion and look up are achieved.

Ternary Tree

It is a type of tree data structure in which each node can have a maximum of three child nodes, commonly referred to as “left,” “mid,” and “right.”

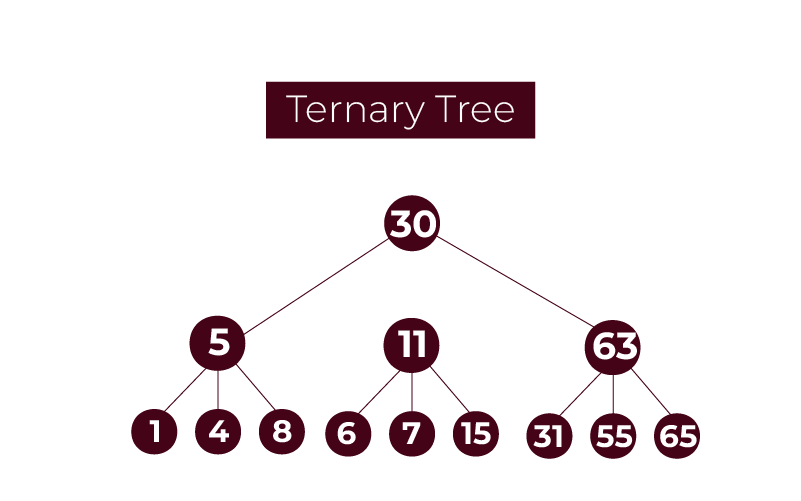
Types of Ternary Tree

Ternary Search Tree(TST)

A ternary tree, more specifically known as the tree data structure, is a tree in which the maximum number of children that can be produced is three.While the binary trees have two children for every node, ternary trees take this constraint as flexible.e binary trees with two children per node,  ternary trees allow more flexibility in organizing data. Ternary tree also has different types and their main aspects are described below.

• The “left” pointer directs to the node with a value smaller than the current node.
• The “equal” pointer directs to the node containing the same value as the current node.
• The “right” pointer guides to the node with a value greater than the current node’s.

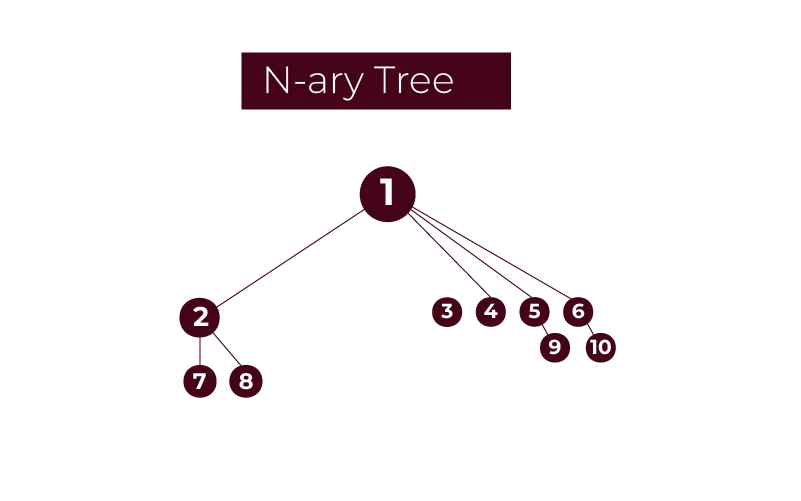
N-ary  Tree (Generic Tree)

An N-arey tree, also called a Generic Tree, is a type of tree data structure. In an N-ary tee, each node holds data records and references to its children. This prohibits duplicate references among its children.

Let’s discuss the features of the N-ary tree:

• Each node can have multiple children
• The exact number of children for each node is not predetermined and varies.

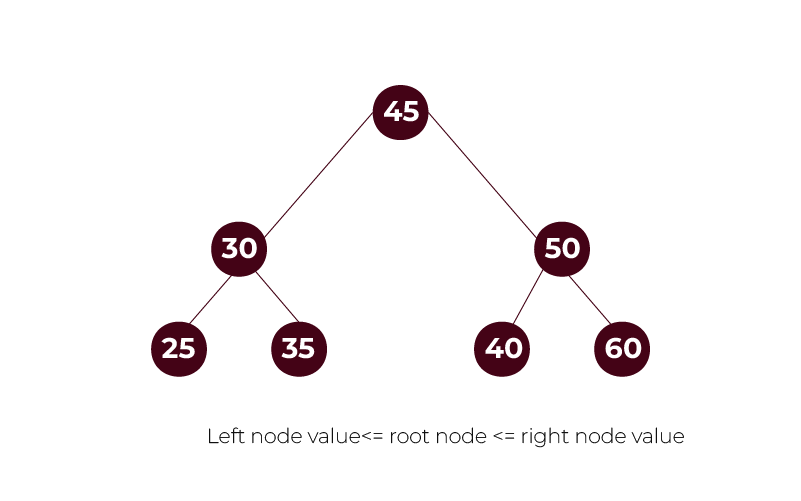
Binary Search Tree

A binary search tree (BST) is a type of binary tree in which each node has at most two children. It follows specific properties that make searching for values efficient. The value of the left child in a binary search tree is always smaller than that of the parent node, and the value of the right child is larger than that of the parent node in the binary search tree.

Also Read: Introduction to Binary Search Trees

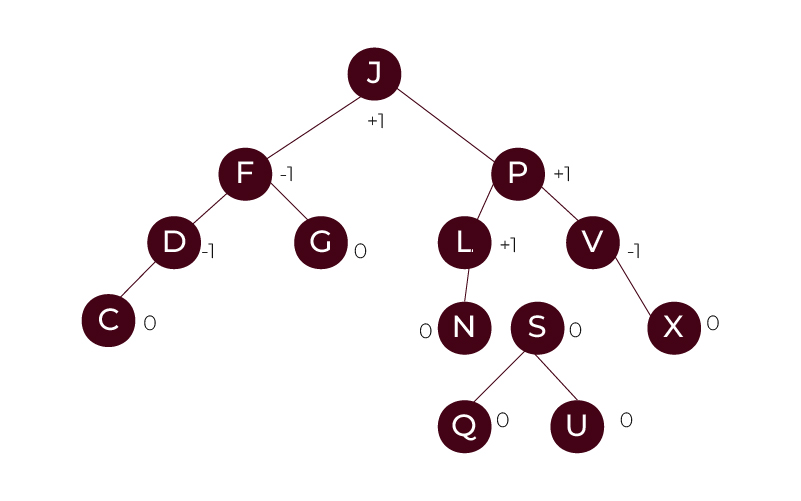
AVL Tree

An AVL Tree is a type of a Binary Search Tree that rebalances itself, or a self ordered tree in which the difference of the heights of the left and right subtrees is. It is called the balance factor that always is kept within a certain range when using this type of makecoils. This type of tree is called the Adelson-Velsky and Landis tree as these two invented this data structure in 1962

Also Read:  AVL Tree in Data Structure

• If the right subtree is one level higher than the left subtree of a node, then the balancing factor value of that node is -1.
• If the left and right subtrees are at the same level, the balancing factor value is 0.
• If the left subtree is one level higher than the right subtree, then the balancing factor is 1.

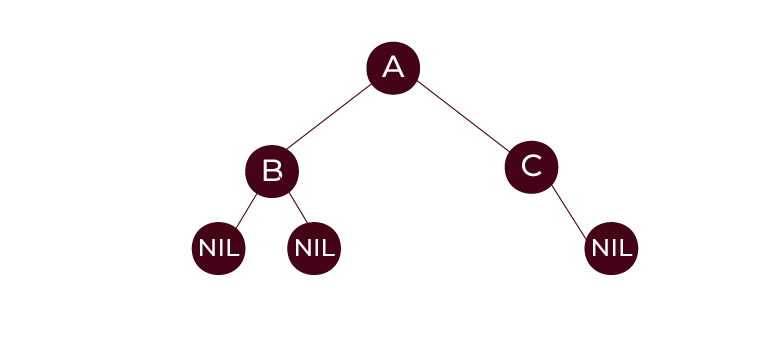
Red-Black Tree

The red-black tree is also a self-balancing tree. Each node is either painted red or black.  The rules of a red-black tree are.

• The leaf nodes and root nodes are black.
• If a parent node is red, both children nodes are black.
• There cannot be two adjacent red nodes.
• Every path from a node to the descendant NULL node (end of the path) must have an equal number of black nodes.

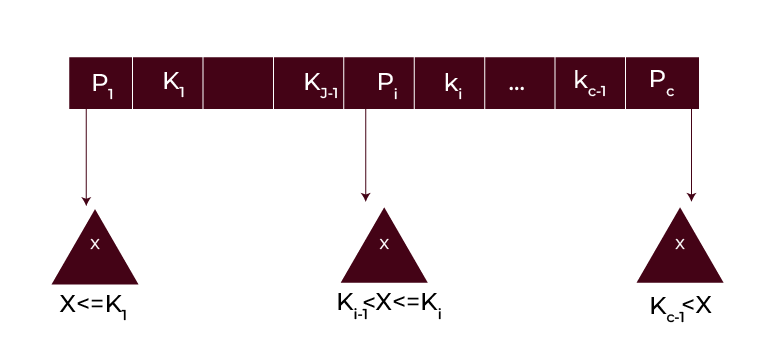
B-Tree

A B-Tree is a self-balancing search tree that is specifically designed for disk storage systems. Let’s understand the key properties of a B-Tree.

• Uniform Leaf Level: The all levels of a B-Tree are guaranteed to be at the same level, It ensures efficient retrieval operations regardless of the tree’s size.

• Minimum Degree ‘t’ : The structure of a B-Tree is determined by its minimum degree ‘t’, which is influenced by the disk block size.

• Key Constraints: Each non-root node must  contain at least t-1’ keys, while the root may have a minimum of one key. The additionally, all nodes including the root, can hold at most ‘(2*t -1)’ keys.

• Child-Node Relationships: The number of children of a node is equal to the number of keys it contains plus one.

• Sorted Keys: The keys within a node are always sorted in increasing order, facilitating efficient searching operations.

• Leaf Node Insertion: The new key insertion in a B-Tree occurs exclusively at leaf nodes, maintaining the balanced structure of the tree.

B+ Tree

A B+ Tree is considered as the enhanced form of self-organizing trees used in database and file organizing techniques to store data and to search for it. It is a variant of the B-Tree and performs especially well in those systems that require writing large portions of data at once, such as large amounts of disk. It is a variation of the B-Tree and is particularly well-suited for  systems that read and write large blocks of data, such as disk storage.

The key characteristics of a B+ tree include.

• Leaf Node Structure: The Leaf nodes in a B+ tree store all key values along with their corresponding data pointers to disk blocks.

• Internal Node Structure: The internal nodes of a B+ tree consist of tree pointers and key values. Each internal node follows a specific structure where keys are stored in ascending order, facilitating efficient search operations.

• Tree Pointer Arrangement: The internal nodes have a maximum of ‘a’ tree pointers, where ‘a’ is the order of the B+ tree. It contains at least two tree pointers,  while other internal nodes have at least [a/2].

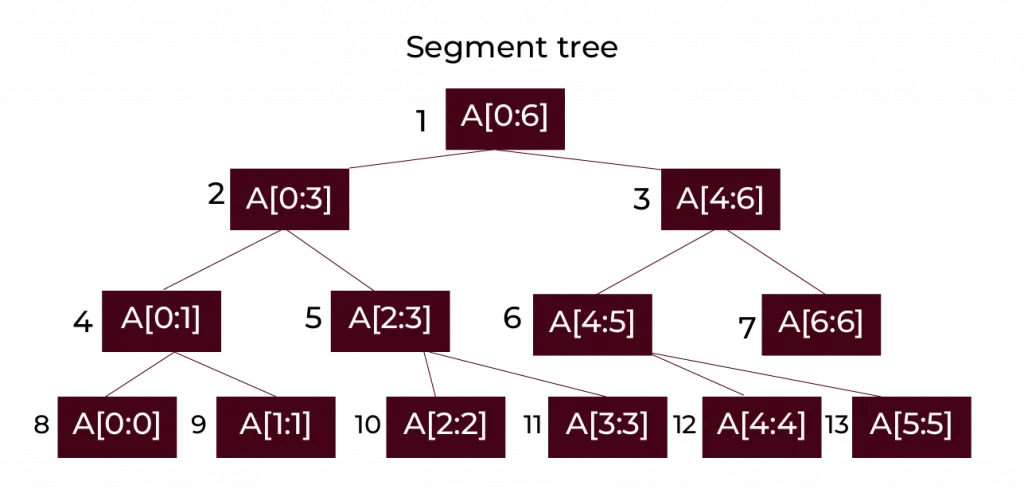
Segment Tree

A Segment tree is a data structure that is used for efficiently answering range queries and handling updates on an array. This is especially useful when you need to perform operations like sum, minimum, greatest common division (GCD), or other associative operations over a range of elements in an array, and also need to update individual elements.

Also Read:  Application of Data Structures

Conclusion

Tree structures stand as central to the concept of data structures when designing as well as implementing. Beginning from the simple binary tree to B-trees, Tries each tree has its own positives that make them suitable for certain applications.Knowledge of these types is useful when deciding on the algorithms or systems that shall provide the needed data hierarchy. If you want to dig deep into Data Structures and Algorithms, Hero Vired’s Certificate Program in Application Development is the perfect choice for you. Enroll now!