Recursion in Python – Explained Simply with Code Examples

Updated on August 13, 2024

Article Outline

Detailed Types of Recursion in Python Comprehensive Look at Benefits and Drawbacks of Using Recursion in Python Diverse Code Examples of Recursion in Python Comparing Recursion and Iteration in Python Extensive Real-World Applications of Recursion in Python Conclusion FAQs

Recursion is the process by which a function calls itself repeatedly to solve a problem. It is one of the most amazing ideas in programming to simplify and improve the efficiency of solving a wide range of challenges. Recursion can improve the overall look of our code and make it look less complex.

Assume that you are attempting to navigate a maze. But instead of walking around aimlessly, a person can just split the entire maze into parts and try to find the solution to each part separately. This is something similar to what recursion does. By decomposition of a problem, we are able to look at it in bits and try to solve every bit as we build up. Although it may seem a little complicated at first, if you use it, this is one of the most effective but straightforward strategies.

Also read: Learn Python Programming Language

Detailed Types of Recursion in Python

Recursion in Python can be classified into two main categories: direct recursion and indirect recursion. Each of these has its subtypes and unique characteristics.

Direct Recursion

Direct recursion occurs when a function calls itself directly. There are several subtypes of direct recursion:

1. Tail Recursion

Tail recursion happens when the recursive call is the last thing the function does. This means there’s nothing left to do after the recursive call returns. Tail recursion is often easier for the compiler to optimise.

def tail_factorial(n, result=1):
    if n == 0:
        return result
    else:
        return tail_factorial(n - 1, n * result)
# Taking user input
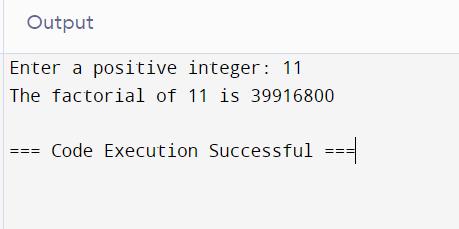
num = int(input("Enter a positive integer: "))
if num < 0:
    print("Factorial is not defined for negative numbers.")
else:
    print(f"The factorial of {num} is {tail_factorial(num)}")

Output:

2. Head Recursion

Head recursion is the opposite of tail recursion. Here, the recursive call is the first thing that happens. The function processes the recursive call before doing any other work.

def head_factorial(n):
    if n == 0:
        return 1
    else:
        return n * head_factorial(n - 1)
# Taking user input
num = int(input("Enter a positive integer: "))
if num < 0:
    print("Factorial is not defined for negative numbers.")
else:
    print(f"The factorial of {num} is {head_factorial(num)}")

Output:

3. Tree Recursion

Tree recursion occurs when a function makes multiple recursive calls. This creates a tree-like structure of calls.

def tree_fibonacci(n):
    if n <= 1:
        return n
    else:
        return tree_fibonacci(n - 1) + tree_fibonacci(n - 2)
# Taking user input
num = int(input("Enter a non-negative integer: "))
if num < 0:
    print("Fibonacci is not defined for negative numbers.")
else:
    print(f"The {num}th Fibonacci number is {tree_fibonacci(num)}")

Output:

4. Nested Recursion

Nested recursion involves a function calling itself with a recursive call as one of its arguments.

def find_max(lst):
    if len(lst) == 1:
        return lst[0]
    else:
        max_of_rest = find_max(lst[1:])
        return max(lst[0], max_of_rest)
# Taking user input
lst = list(map(int, input("Enter a list of numbers separated by spaces: ").split()))
if not lst:
    print("The list is empty.")
else:
    print(f"The maximum element in the list is {find_max(lst)}")
This function recursively finds the maximum

Output:

Indirect Recursion

Indirect recursion occurs when a function calls another function, which in turn calls the original function. This can create a cycle of function calls.

def is_even(n):
    if n == 0:
        return True
    else:
        return is_odd(n - 1)
def is_odd(n):
    if n == 0:
        return False
    else:
        return is_even(n - 1)
# Taking user input
num = int(input("Enter an integer: "))
print(f"{num} is even: {is_even(num)}")
print(f"{num} is odd: {is_odd(num)}")

Output:

Get curriculum highlights, career paths, industry insights and accelerate your technology journey.

Download brochure

Comprehensive Look at Benefits and Drawbacks of Using Recursion in Python

Benefits of Using Recursion

Simplifies Complex Problems

Break down large problems into smaller, manageable pieces.
Each part can be solved individually, making the code easier to write and understand.
Ideal for problems like tree traversals or generating permutations.

Cleaner and More Elegant Code

Achieves results with fewer lines of code compared to multiple loops and conditional statements.
It makes the program easier to read and maintain.

Natural Fit for Certain Problems

Suits hierarchical structures like trees and graphs.
Provides an intuitive way to navigate these structures, aligning with the problem’s nature.

Ease of Sequence Generation

Simplifies generating sequences like the Fibonacci series.
Enables defining the base case and recursive step, thereby automating the sequence generation process.

Drawbacks of Using Recursion

Higher Memory Usage

Recursion can lead to higher memory usage as each recursive call adds a new layer to the call stack, consuming memory.
This can become problematic for deep recursion levels, potentially leading to stack overflow errors.

Slower Execution Time

Recursive functions can be slower than their iterative counterparts due to the overhead of multiple function calls.
Each call consumes time and resources, making recursion less efficient for some tasks.

Difficulty in Debugging

Debugging recursive functions can be challenging as tracing the flow of recursive calls and understanding the state of each call can be difficult, especially for complex problems.
This can lead to errors that are hard to identify and fix.

Risk of Infinite Recursion

Without a proper base case, a recursive function can call itself indefinitely, leading to infinite recursion.
This can crash the program and cause a stack overflow. Ensuring a well-defined base case is crucial to prevent such issues.

Not Always Intuitive

For beginners, recursion can be less intuitive than iterative solutions.
For beginners, grasping how a function calls itself and how the call stack operates can be quite challenging. Iteration, with its straightforward loop constructs, can often be easier to grasp initially.

Diverse Code Examples of Recursion in Python

Calculating the Greatest Common Divisor (GCD) with Recursion

def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)
num1 = int(input("Enter the first positive integer: "))
num2 = int(input("Enter the second positive integer: "))
print(f"The GCD of {num1} and {num2} is {gcd(num1, num2)}")

Output:

Reversing a String Recursively

def reverse_string(s):
    if len(s) == 0:
        return s
    else:
        return s[-1] + reverse_string(s[:-1])
string = input("Enter a string: ")
print(f"The reverse of '{string}' is '{reverse_string(string)}'")

Output:

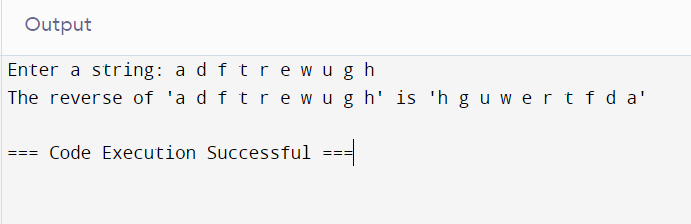
Comparing Recursion and Iteration in Python

Aspect	Recursion	Iteration
Control Flow	Control flow is handled through function calls, making the process more intuitive for problems that naturally fit a recursive approach.	Control flow is managed with loops (for, while), which can be more straightforward for simple repetitive tasks.
Memory Usage	Uses more memory due to the call stack. Each recursive call consumes stack space, which can lead to a stack overflow if the recursion depth is too great.	Generally, it uses less memory since it doesn’t involve multiple function calls. Loops handle the iterations within a single function call.
Readability	Often results in cleaner and more elegant code for problems like tree traversal and sequence generation. The logic is expressed directly in the recursive function.	This can be easier to understand for those new to programming. Loop constructs are more familiar and less abstract than recursive calls.
Performance	It can be slower due to the overhead of multiple function calls. Each call adds to the call stack, increasing the time complexity.	It is typically faster since it avoids the overhead of function calls. The loop executes within a single function frame, making it more efficient.
Suitability	Ideal for problems that can be divided into similar sub-problems, like factorial computation, Fibonacci sequence, and tree/graph traversal.	Better for tasks with a known number of repetitions or when performance is critical, like processing arrays and lists.

Code Example: Recursive Approach

def recursive_sum(n):
    if n == 0:
        return 0
    else:
        return n + recursive_sum(n - 1)
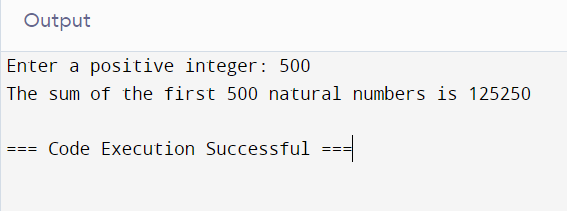
num = int(input("Enter a positive integer: "))
print(f"The sum of the first {num} natural numbers is {recursive_sum(num)}")

Output:

Code Example: Iterative Approach

def iterative_sum(n):
    total = 0
    for i in range(1, n + 1):
        total += i
    return total
num = int(input("Enter a positive integer: "))
print(f"The sum of the first {num} natural numbers is {iterative_sum(num)}")

Output:

Extensive Real-World Applications of Recursion in Python

Mathematical Calculations

Recursion simplifies many mathematical calculations. Examples include:

Calculating the factorial of a number
Generating the Fibonacci series

Data Structures

Traversing data structures like trees and graphs is another area where recursion excels. Examples include:

Searching nodes in a binary tree
Inserting and deleting nodes in a binary tree

File System Operations

Recursion is often used in file system operations. Examples include:

Searching directories
Copying files
Recursively traversing a directory tree to access each file and folder

Combinatorial Problems

Recursion is beneficial for solving combinatorial problems. Examples include:

Generating permutations
Generating combinations

Backtracking Algorithms

Recursion is key to implementing backtracking algorithms, which solve problems by trying different solutions and undoing steps if they don’t work. Examples include:

The N-Queens problem
Solving mazes

Sorting Algorithms

Many sorting algorithms use recursion as part of their strategy. Examples include:

Quicksort
Mergesort

AI and Machine Learning

In AI and machine learning, recursion helps build decision trees and implement algorithms, which are crucial for navigating and analysing data structures in AI models.

Depth-first search (DFS)
Breadth-first search (BFS)

Conclusion

In this blog, we explored the concept of recursion in Python. It breaks down a problem into simpler sub-problems, which makes the code more efficient and easier to manage. As with any method, there are issues associated with recursion, such as increased memory demand and possible slower speed. However, learning to recognise the good application of recursion as a tool in programming can be helpful in improving our problem-solving capabilities. Recursive problem-solving skills are useful when solving different programming tasks; for this reason, mastering recursion proved to be very useful.

FAQs

What are the common problems that can be solved using recursion?

Common problems solved using recursion include:

Calculating factorials
Generating Fibonacci series
Traversing tree and graph structures
Performing file system operations
Solving combinatorial problems like permutations and combinations
Implementing sorting algorithms like quick-sort and merge-sort

How can I avoid infinite recursion in my Python programs?

To avoid infinite recursion, make sure the base case for your recursive function is clearly specified and terminates the recursion.

What are the disadvantages of using recursion in Python?

Disadvantages of recursion include:

Higher memory usage due to the call stack
Slower execution time compared to iterative solutions
Difficulty in debugging and understanding the flow of recursive calls
Risk of stack overflow if the base case is not properly defined

Updated on August 13, 2024

Link

Programs tailored for your success

Popular

Management

Data Science

Finance

Technology

Future Tech

3 ASSURED INTERVIEWS

Accelerator Program in

Business Analytics and Data Science

With

Part-time · 10 months

Apply by : 30 October, 2024

Financial Analysis, Valuation, & Risk Management

3 ASSURED INTERVIEWS

Certificate Program in

Financial Analysis, Valuation, & Risk Management

With

Part-time · 7 months

Apply by : 30 October, 2024

INTERNSHIP ASSURANCE

Certificate Program in

DevOps & Cloud Engineering

With

Part-time · 7.5 months

Apply by : 30 October, 2024

Upskill with expert articles

View all

Hero Vired is a leading LearnTech company dedicated to offering cutting-edge programs in collaboration with top-tier global institutions. As part of the esteemed Hero Group, we are committed to revolutionizing the skill development landscape in India. Our programs, delivered by industry experts, are designed to empower professionals and students with the skills they need to thrive in today’s competitive job market.

Data Science

Accelerator Program in Business Analytics & Data Science

Integrated Program in Data Science, AI and ML

Accelerator Program in AI and Machine Learning

Advanced Certification Program in Data Science & Analytics

Certification Program in Data Analytics

Technology

Certificate Program in Full Stack Development with Specialization for Web and Mobile

Certificate Program in DevOps and Cloud Engineering

Certificate Program in Application Development

Certificate Program in Cybersecurity Essentials & Risk Assessment

Finance