Expression Tree in Data Structure: A Comprehensive Guide

In data structures, expression trees provide the possibility to work with mathematical expressions which are convenient to represent. Such trees are binary, meaning every node contains an operand – a constant or a variable – while a non-terminal node contains an operator like +, -, *, or /. If expressions are structured in this manner, evaluation is faster compared to the normal string-based methods, because trees control operator precedence and parentheses. This efficiency is particularly desirable for compilers, databases as well as symbolic computation systems.

What is an Expression Tree?

Mathematical expressions are represented as binary trees which are called expression trees. Operands of constant/variables are represented by each leaf node, whereas non-leaf nodes are operators like +, -, *, or /. Computing is largely based on the ability to run expressions, so expression trees are important as they make expression evaluation and processing much more efficient than string processing built from physical tokens without type information.

• Infix Expression: An equality is made between operands (a + b). This is the most common form humans use, but computers cannot process it easily, there are varying operator precedence and parentheses.
• Prefix Expression (Polish Notation): An operator comes before its operand (eg, +ab). For an order of operations, prefix notation drops the need for parentheses.
• Postfix Expression (Reverse Polish Notation): Operators take their operands (e.g., ab+, so), making an operator produce an answer, rather than an input to an operation. It doesn’t require parentheses, and simplifies the computation of expressions, like prefix notation does.

Also Read:  Introduction to Tree Data Structure

Expression Tree Structure:

An expression tree is a binary tree where:

• An operand (constant or variable) is contained at each leaf node.
• An operator is associated with each non-leaf node.
• Subexpressions to be evaluated before applying the operator at root are represented by left and right subtrees respectively.

Example Expression: (a – b) * (c + d)

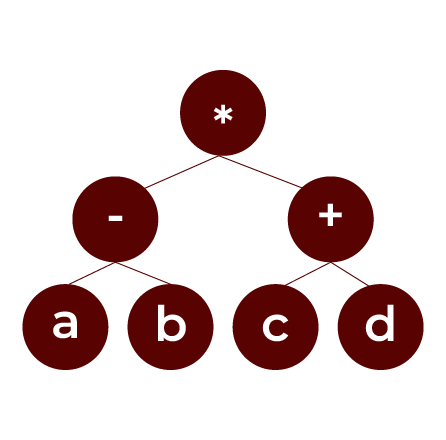
Evaluating Expressions Using an Expression Tree

The result of an arithmetic expression can be computed using a post-order Traversal of expression tree. Typically, postorder traversal is used for evaluating expressions:

• In the case of the left subtree, do the same operation and repeat step 1.
• This right subtree is also recursively reduced as shown next, starting with the left sub-tree node.
• Apply the operator at the root to the results obtained from the first two steps of the method.

Also Read: Types of Trees in Data Structure

Algorithm:

For the tree representing (a – b) * (c + d), this algorithm recursively computes the values of the sub-expressions.

Construction of Expression Trees:

From Prefix and Infix Expression:

To construct an expression tree from a prefix and infix expression:

• It reads the prefix expression from left to right, the first element is the root.
• Recording of infix expression is continued to place operant and operators respectively to build up subtrees, recursively.

From Infix and Postfix Expression:

When given infix and postfix expressions:

• From the postfix expression, the root starts from the last element of it.
• Continuing recursively, the infix expression is scanned to divide the left and right subtrees.

From a Postfix Expression:

For a postfix expression alone:

• Go from left to right through the expression.
• The operands/operators push operands to a stack, the operators pop the last two operands from the stack, create a new subtree, and return a result into the stack.

Also Read: Application of Data Structures

Pseudocode:

C++ Code for Constructing an Expression Tree

Output:

Why Stack is Essential in Expression Tree Construction

The stack has a crucial role in making sure that the expression tree is built by the rules of the operator precedence and associativity. Through stack tracking of nodes and correct pairing of operands to operators, the stack can efficiently track nodes during postfix or prefix expression evaluation. Without the stack, we would have errors in constructing a tree from a linear expression, especially with complex expressions having nested operations.

Put simply, expression trees are useless without stack operations. They give a way to organize and manage the nodes well so that the tree structure reflects exactly what was being expressed.

Main Functions of Stack in Tree Implementation

A stack is used when constructing an expression tree since the number of operands and operators are bounded at all times. The stack is critical to the fact that the proper operands are associated with their respective operators as the tree is being built. Below are the key stack operations and their functions within the context of expression tree construction:

Push

Function: Pushes an element (nearly always a node) at the top of the stack.

Explanation: In the construction of expression tree nodes are pushed which represent operands (numbers, variables, constants…) on the stack. It serves us to store operands temporarily until they could be connected to some operator. The tree structure is organized by “saving” nodes until the correct operator node can be found, and then the operand node nodes are restored to their position in the tree.

Pop

Function: Removes the top element from the stack and returns it.

Explanation: An operator is processed during an expression and so needed operand nodes must ‘pop’ off the stack. The children of the operator node are these operands and then they are used as operands. If the pop operation was not used in the building of the tree’s hierarchy, operators would not know where they fit within the hierarchy of the tree, operators would not know what operand to work with, and operations could not be performed in the correct order.

Peek (Top)

Function: On views the top element of the stack without it being popped.

Explanation: Inspecting the most recently added node without modifying the stack is useful using Peek. Sometimes when we are to determine the next operation or to check for the precedence of the operators, it becomes very important. As an example, peek can assist in managing operator precedence so the tree is determined by the actual order of operations (i.e., multiplication ahead of addition).

IsEmpty

Function: Checks if the stack is empty.

Explanation: It is a must that we make sure before performing a pop operation, that the stack possesses some elements so that we do not “underflow” error. This takes care of the case in expression tree construction where it fails to find enough operands to assign against the operator. It also prevents errors which can occur as a result of popping from an empty stack.

Size

Function: It returns the number of elements in a stack.

Explanation: It is useful to know how big the stack is to understand how many are in the tree during the construct tree process. Furthermore, it’s also nice when debugging and verifying that you expect each stage of your algorithm to contain the correct number of operands and operators. It’s useful for initial stack size monitoring to avoid some issues such as running out of allocated memory or getting lost of nodes during tree construction.

Also Read: What is Stack in Data Structures

Traversing Expression Trees:

Traversals are crucial for converting expressions between different formats (prefix, infix, postfix).

• Preorder Traversal (Prefix Expression): Start with the root node, and then go down to the left and right and repeat this process.
• Inorder Traversal (Infix Expression): Starting with the left subtree perform pre-order traversal, the current node is the root, perform pre-order traversal in the right subtree.
• Postorder Traversal (Postfix Expression): Start from the left or right subtree and come back, then come directly to the root node.

Example: Given the tree for (a – b) * (c + d):

• Preorder (Prefix): *-ab+cd
• Inorder (Infix): (a – b) * (c + d)
• Postorder (Postfix): ab-cd+*

Applications of Expression Trees

Expression trees are used in various domains, particularly where the evaluation and optimization of expressions are necessary:

Compiler Design

Tree expressions are not used in compilers to produce intermediate code for arithmetical expressions only, but also they are used frequently for this purpose. In fixing up the notations of infix expression to expression trees, further manipulations on the outcome generated can be done effectively within the compiler such as eradicating repetitive sub-operations and optimizing the sequences of instructions in the event.

Database Query Processing

In working with systems employing relational databases the expression trees are used to construct query execution plans. Expression trees, together with other structures, are used by the DBMS to order SQL queries as well as joins, selections, and projections. A graph expression tree helps the system select the best way to process the query through the rearrangement of the operations.

Symbolic Computation

MATLAB, Mathematica, and SymPy use expression trees for expression manipulation and for the computation of mathematical expressions. These trees are used to carry out mathematics such as first and second derivative, integration, simplification, and solving of equations.

Expression Evaluation in Interpreters

Up to this point, the function of expression evaluation was the exclusive right of the target language’s interpreter.

Programmers using programming languages like Python and JavaScript utilize expression trees to evaluate arithmetic and logical expressions formulated at runtime.

Complexity Analysis

It is important to understand the time and space complexity of building, and using, expression trees, when dealing with large datasets or complex expressions. Below is the complexity breakdown for expression tree construction:

Time Complexity

The number of nodes makes the time complexity of constructing an expression tree, therefore, in the number of operands and operators in the expression.

• Linear Time: The construction of the expression dominates the time of O(n) for n the number of tokens (operands and operators) in an expression. That’s because there is a need to process every token once (either on a stack or in the tree). On top of this, the tree itself requires a constant amount of work for each token.

Space Complexity

The expression tree’s space complexity is also O(n) where n is several tools in expression. This complexity arises from two main factors:

• Tree Storage: Each node is required to store the dictionary of the operands we have in the tree structure itself, which means that, in the tree structure itself, we need to have storage for each node (operator and operand nodes). So the tree will have one node per token in the expression, and have a space requirement of order n.
• Recursion Stack: In the case of the traverse (either for construction or evaluation), we must keep a recursion stack. The worst-case depth of the recursion stack is proportional to the height of the tree and can be a large order of n for expressions having only one chain of operations (such as a long one of multiplications or additions).

Also Read: Top Data Structure Interview Questions and Their Answers

Evaluation Complexity

Once constructed, the evaluation of an expression tree has the following complexity:

• Traversal Complexity: The time complexity becomes O(n), as we only traverse the tree once, to compute (or the ability to evaluate, convert to postfix/infix notation, as examples) and visit each node.
• Memory Overhead: Evaluation or construction also takes O(n) space, as it is stored on the stack that it uses during evaluation or construction.

Conclusion

Expression trees are important in managing, evaluating, constructing and manipulating mathematical expressions. Organizations of expressions properly help in offering a more effective way to handle operations hierarchically especially using a stack in directing the operations of operators. Both in compilers, database queries and symbolic computation, expression trees serve to simplify and optimise the evaluation of expressions in a way that is extremely useful for precision and efficiency. Huge and even complex expressions can be evaluated thanks to the fact that these data structures possess linear time and space characteristics. If you want to learn about this in more detail, the Certificate Program in Application Development powered by Hero Vired is the perfect choice for you.