Developing computer algorithms and data structures has been closely associated with asymptotic notation. It is applied to understand and facilitate the development of simple and complex algorithms, from searching and sorting to data processing and machine learning. This article will explain what asymptotic notation is and its properties, examples, and types. Data structures with asymptotic notation provide a bridge for evaluating data structure algorithm complexity in a standard and theoretical way and for algorithm comparison among practical applications.
What is Asymptotic Analysis?
The tools of asymptotic notation form a convenient, yet formally rigorous way to discuss the efficiency and scalability (or ‘complexity’) of algorithms in computer science. An algorithm is described by them, giving a high-level understanding of what happens as input size increases. They answer the question: As the input size grows, what changes about an algorithm’s runtime or space requirements? It tells how fast an algorithm will run in terms of best case (minimum time), average case, and worst case (maximum time) by computing the time an operation takes to run in mathematical units.

Get curriculum highlights, career paths, industry insights and accelerate your technology journey.
Download brochure
Importance of Asymptotic Analysis in Data Structure
- The asymptotic notation (only concerned with the largest) sorts algorithms by how well they perform as the problem grows.
- It teaches us how an algorithm works as our data gets more complicated, which is important for scalability.
- It’s used to predict how an algorithm will behave under variable conditions.
- First, it abstracts some special details, such as the hardware and implementation nuances, to allow for a fair comparison of different approaches.
- Asymptotic notation can be useful for evaluating efficiency and resource constraints and making better decisions.
Types of Asymptotic Notations in Data Structure
There are three following types of asymptotic notations:
- Big O Notation
- Omega Notation
- Theta Notation
Big-O Notation (O)
A mathematical concept in computer science about the upper bound of an algorithm’s time or space complexities is big O (or big O notation). It gives you a worst-case scenario of how an algorithm behaves by increasing input size.
Big O Notation in Mathematical Representation.
If there exist positive constants c0 and c1 so that 0 ≤ f(n) ≤ c0*g(n) for all n ≥ c1, we say that f(n) is O(g(n)). In other words, for n big enough, function f(n) is not growing more than function g(n) times by a constant factor.
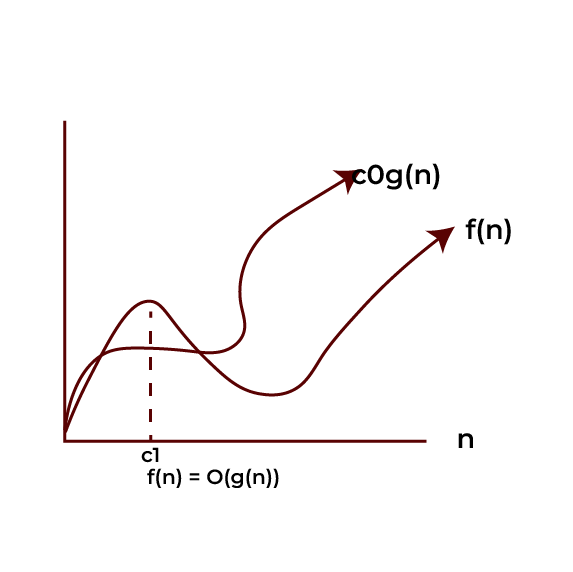
O(g(n)) = {f(n): there exist positive constants c0 and c1 such that 0 ≤ f(n) ≤ c0g(n) for all n ≥ c1}.
Omega Notation(Ω)
For example, we write down the lower bound of the algorithm’s running time using omega notation, which indicates the algorithm’s least running time. As a result, it has the best-case complexity of any algorithm.
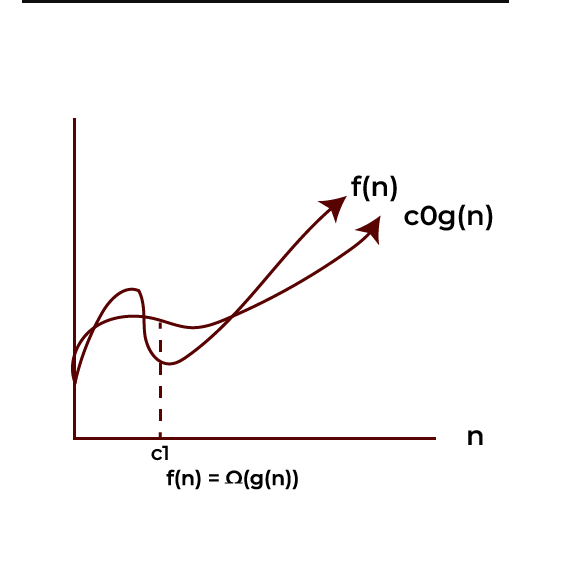
Ω(g(n)) = {f(n): there exist positive constants c0 and c1, such that 0 ≤ c0g(n) ≤ f(n) for all n ≥ c1}.
Theta Notation(θ)
The algorithm’s average bound is described using theta notation, which is an upper and lower bound function that represents exact asymptotic behaviour.
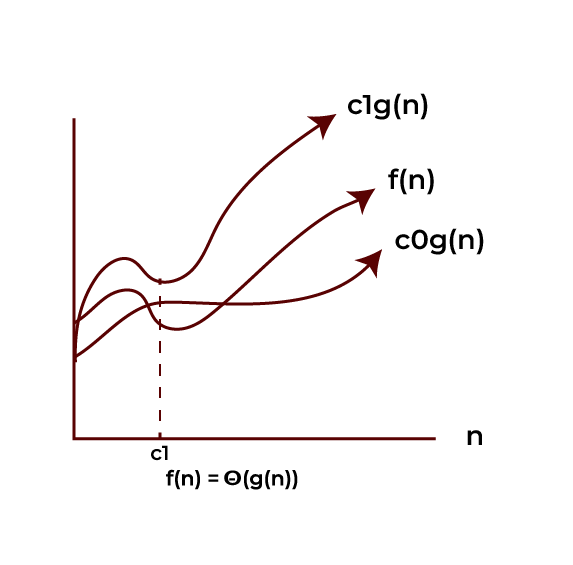
Θ(g(n)) = {f(n): there exist positive constants c0, c1 and c2, such that 0 ≤ c0g(n) ≤ f(n) ≤ c1g(n) for all n ≥ c2}
Also Read: Arrays in Data Structure
Difference Between Big-O Notation, Omega Notation, and Theta Notation
| Parameter |
Big O Notation (O) |
Omega Notation (Ω) |
Theta Notation (Θ) |
| Definition |
outlines a maximum limit on an algorithm’s time or space complexity. |
gives a lower bound on an algorithm’s time or space complexity. |
gives the time or space complexity’s upper and lower bounds. |
| Purpose |
used to describe an algorithm’s worst-case situation. |
used to describe an algorithm’s best-case situation. |
used to describe the exact bound of an algorithm (both best and worst cases). |
| Interpretation |
shows the algorithm’s maximum rate of complexity growth. |
shows the algorithm’s minimum rate of complexity growth. |
shows the precise rate at which the complexity of the algorithm is increasing. |
| Mathematical Expression |
f(n) = O(g(n)) if ∃ constants c > 0, n₀ such that 0 ≤ f(n) ≤ c*g(n) for all n ≥ n₀. |
f(n) = Ω(g(n)) if ∃ constants c > 0, n₀ such that 0 ≤ c*g(n) ≤ f(n) for all n ≥ n₀. |
f(n) = Θ(g(n)) if ∃ constants c₁, c₂ > 0, n₀ such that 0 ≤ c₁g(n) ≤ f(n) ≤ c₂g(n) for all n ≥ n₀. |
| Focus |
emphasises performance limits (less efficient aspects). |
emphasises performance at the lower limit (more efficient aspects). |
gives a fair assessment of performance by concentrating on upper and lower bounds. |
| Usage in Algorithm Analysis |
Efficiency analysis, particularly about worst-case performance, is a common application. |
used to illustrate efficacy in ideal circumstances. |
used to give an accurate analysis of the efficiency of algorithms in common situations. |
| Common Usage |
predominant in worst-case analysis applications, both theoretical and practical. |
Though less frequent than Big O, it is crucial to comprehend optimal efficiency. |
utilised when an algorithm performs consistently when given a variety of inputs. |
| Examples |
O(n) is the search time in an unsorted list. |
To add an element to a sorted array, use Ω(1). |
The element in a sorted array is always in the middle of a linear search: Θ(n). |
Limitations of Asymptotic Analysis
- We assume large input sizes, which can be regarded as tending to infinity; however, real-world inputs may not always be large enough.
- The algorithm’s growth rate is not considered; only larger terms are considered, while smaller ones are ignored.
- It gives an exact running time upper bound, but its analysis approximates how asymptotically good the running time is as the input size grows.
- Usually, it focuses on running time and lessens other resources (memory, e.g.) unless the problem is space-complex.
- When the coefficient of the dominant term is ignored, algorithms that differ only in their dominant term are regarded as identical.
- Some algorithms, such as randomised ones and algorithms with complex control structures, may not play natively with classical asymptotic analysis.
Also Read: Application of Data Structures
Properties of Asymptotic Notation in Data Structure
Asymptotic notations follow certain properties that help analyse and compare function growth. These properties can be proven using the fundamental equations of each notation.
General Property:
- In Big O Notation (O), we use the upper bound for the growth rate of some functions.
- It’s Big Omega (Ω) notation and means a lower bound.
- A Big Theta (Θ) is a function that grows at the same rate as another.
Transitive Property:
Instead of comparing the growth rates of f(n), g(n), and h(n), it compares the growth rates of two functions f(n) and g(n).
Reflexive Property:
As defined above, the reflexive property should be stated that any function f(n) has its asymptotic bounds for that f(n).
Symmetric Property:
We have used symmetry in the theta-notation which tells that two functions are growing at the same rate.
Transpose Property:
Big-O notation and omega notation have the transpose property related to them.
Also Read: Top Data Structure Interview Questions
Conclusion
Algorithm analysis is a field that makes use of the properties of asymptotic notation, Big O, Omega, and Theta, in quantifying the efficiency of algorithms for large sizes of input. In notations, these factors that don’t depend on the input size are abstract away, thus enabling us to concentrate on the main growth rates of algorithms. Big O notation gives us an upper bound on how an algorithm runs, Omega notation gives us a lower bound, and Theta notation gives us a tight range of growth rates.
With these notations at hand, we know what we are working with, and can make more information-based decisions about selecting, optimising, and scaling algorithm choices, and help contribute to developing more efficient and powerful software approaches. Are you an aspiring data scientist? Take the lead with the Integrated Program in Data Science, Artificial Intelligence & Machine Learning offered by Hero Vired in collaboration with MIT Open Learning.
FAQs
The efficiency of the algorithm is described using asymptotic analysis in that the input size grows. It is concerned with the growth rate of the algorithm's running time or space requirements and gives an abstract way to compare the performance of different algorithms in a theoretical, platform-independent way.
In explaining and comparing the performance of algorithms for large input sizes, asymptotic analysis is used. By doing so, it allows the developers to know what will be the best algorithm to use by its prediction of how well the algorithm will scale. It is critical to make software optimise, and also make applications run as efficiently as possible when working with huge amounts of data.
The running time of an algorithm is represented with big O notations that stand for the upper bound of the algorithm. In doing so, it produces a worst-case scenario envisioning how much time or space an algorithm will consume as the input grows. Consider for example O(n) means the running time gets linear with input size.
The running time of an algorithm is denoted by Ω (Ω) notation, which denotes the lower bound of a given algorithm. It is the best-case scenario, i.e. the minimum amount of time or space an algorithm can consume as the size of input increases. For example, an algorithm is Ω(n) if the runtime is at least linear in the amount of input.
Big O notation is sometimes used because the worst-case number allows an algorithm to guarantee that the algorithm will not take more than a certain amount of time or space. It’s important to do this to make sure systems perform reliably and that they meet the required performance standards under all conditions.
Updated on February 5, 2025



