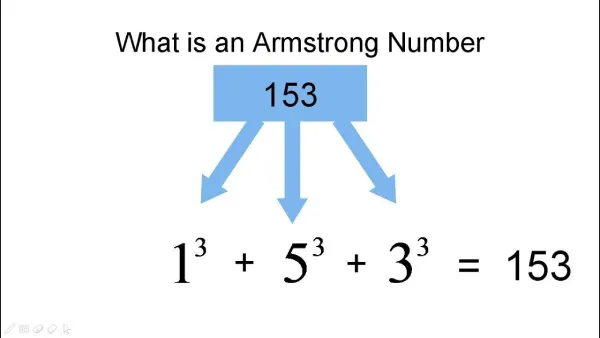
Armstrong Number is a special kind of number in Math. This number equals the sum of digits, each number raised to a power, For example, If you have a number like 153, It is an Armstrong Number Because 1^3 + 5^3 + 3^3 equals 153. Armstrong’s number is also called a narcissistic number or plenary number. In this article, we will check whether the number is Armstrong or not using Python language.
What is the Armstrong Number in Python?
The Armstrong Number in Python is the number that each number raised to power. The sum of digits is equal to that number. For example, 1^3+ 5^3+ 3^3 equals 153.

POSTGRADUATE PROGRAM IN
Multi Cloud Architecture & DevOps
Master cloud architecture, DevOps practices, and automation to build scalable, resilient systems.
Armstrong Number Logic
An Armstrong number is a simple mathematical number. This number has some property. Let’s see how we can find the Armstrong number.
- Take any number from the user. For example, We will take 153 as a number and divide that number into 1, 5, and 3 digits.
- In the next step, we will add each digit to a power equal to the total number of digits in the original number. In this example, we have three digits after adding each number has power, it will look like this 1 ^3, 5^3, and 3 ^3.
- Now, we can calculate the result of each number by adding these raised digits: 1 ^ 3 = 1, 5^3 = 125, and 3 ^3 = 27.
- Finally, we can add those numbers to see the result = 1 + `125 + 27 = 153.
Armstrong Number Algorithm
Armstrong’s Number is also called the Narcissistic number or plenary number. It is a special type of number in Mathematics. In this section, we will use the Armstrong number algorithm. Here’s the Armstrong Number algorithm.
- Take the integer input from the user in the Python program.
- Count the Number of digits. If there is more than one digit, check “Is this number Armstrong or not?”
- Iterate each digit through a loop and raise each digit to the power of the total number of digit
- Then, the sum of those digits.
- In this step, you have to check the sum of the iterated digits and your input number. If you compare those numbers, if they are equal, return “This is an Armstrong number; “ otherwise, return “This is not an Armstrong number.”
Check a three-digit number using a while loop
In this program, we will check whether the number is Armstrong or not using the while loop. We will check the three-digit number.
Source Code
# This code written by Neeraj Kumar
number = int(input("Enter a number: "))
# initialize sum
sum = 0
temp = number
while temp > 0:
digit = temp % 10
sum += digit ** 3
temp //= 10
if number == sum:
print(sum,"is an Armstrong number")
else:
print(sum,"is not an Armstrong number")
Output
Enter a number: 153
153 is an Armstrong number
Also Read: Armstrong Number program
in C

82.9%
of professionals don't believe their degree can help them get ahead at work.
Check the n-digit number using recursion
In this method, we will check whether the number is Armstrong by using the recursion. Recursion is the technique where the function calls itself. The following program demonstrates the Recursion method.
Program
def count_digits(n):
if n == 0:
return 0
return 1 + count_digits(n // 10)
def armstrong_recursive(n, num_digits):
if n == 0:
return 0
return (n % 10)**num_digits + armstrong_recursive(n // 10, num_digits)
def is_armstrong(n):
num_digits = count_digits(n)
armstrong_sum = armstrong_recursive(n, num_digits)
return armstrong_sum == n
num = int(input("Enter a number to check if it's an Armstrong number: "))
if is_armstrong(num):
print(num, "is an Armstrong number.")
else:
print(num, "is not an Armstrong number.")
Output
Enter a number to check if it's an Armstrong number: 153
153 is an Armstrong number.
Check the n-digit numbers using functions
In this section, we will check the Armstrong number in Python using a function. In this example, we created two functions: the sum and the count_digits_fun() function. The following program demonstrates the code.
Program
def count_digits_fun(n):
i= 0
while n> 0 :
n //= 10
i += 1
return i ;
def sum(n):
i = count_digits_fun(n)
s = 0
while n > 0:
digit = n%10
n //= 10
s += pow(digit,i)
return s
value = sum(number) ;
if number == value:
print(value,"is an Armstrong number")
else:
print(value,"is not an Armstrong number")
Output
Enter a number to check if it's an Armstrong number: 153
153 is an Armstrong number.
Check the n-digit numbers using a while loop
In this section, we will find the n-digit Armstrong number using the while. The following program demonstrates the n-digit Armstrong number using a while loop.
Program
number = int(input("Enter the number = "))
digits = len(str(number))
temp = number
add_sum = 0
while temp != 0:
k = temp % 10
add_sum += k**digits
temp = temp//10
if add_sum == number:
print('It is an Armstrong Number')
else:
print('It is not a Armstrong Number')
Output
Enter the number = 8208
It is an Armstrong Number
Conclusion
Armstrong number is an interesting and practical application in Mathematics. In this article, we learned how to create an Armstrong program in the Python Programming language. Implementing Armstrong in Python increases problem-solving skills in Python programming and builds logic implementation. We saw different approaches to building the Armstrong program, such as Recursion and loops. Recursion is the technique where the function calls itself, and the loop uses the iteration approach. If you want to explore Python programming, you can consider the Accelerator Program in Business Analytics and Data Science.
How can I check if a number is an Armstrong number in Python?
Can negative numbers be Armstrong numbers in Python?
Which approach, iteration or recursion, is more efficient for finding Armstrong numbers in Python?
What is an example of Armstrong’s number?
Can Armstrong numbers have more than three digits?
Updated on July 19, 2024
