Are you new to the Python programming language and wondering how it handles basic math operations? Would you like to learn how addition, subtraction, multiplication and other operations within arithmetics work in Python? The following blog helps you understand how to use arithmetic operators to make all these operations as easy as possible to use.
Now, let us see some of the arithmetic operators in Python that will make your journey of coding much smoother.
List of Arithmetic Operators Available in Python
Python includes a set of arithmetic operators used to perform mathematical calculations. These operators are essential tools for any programmer. Here’s a quick rundown of the arithmetic operators available in Python:
- Addition (+): Adds two numbers.
- Subtraction (-): Subtracts the second number from the first.
- Multiplication (*): Multiplies two numbers.
- Division (/): Divides the first number by the second.
- Modulus (%): Returns the remainder when the first number is divided by the second.
- Exponentiation (**): Raises the first number to the power of the second.
- Floor Division (//): Divides the first number by the second and rounds down to the nearest whole number.
Let’s look at each of these operators in more detail with some unique examples.
Also read: What are Python Functions

POSTGRADUATE PROGRAM IN
Multi Cloud Architecture & DevOps
Master cloud architecture, DevOps practices, and automation to build scalable, resilient systems.
Detailed Explanation of Each Arithmetic Operator with Unique Examples
Addition Operator (+)
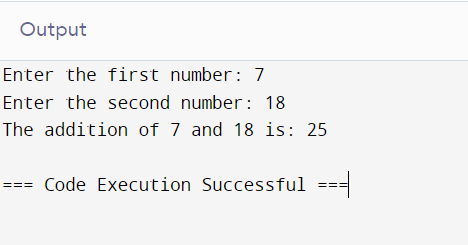
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Using the addition operator
result = num1 + num2
# Displaying the result
print(f"The addition of {num1} and {num2} is: {result}")
Output:
Subtraction Operator (-)
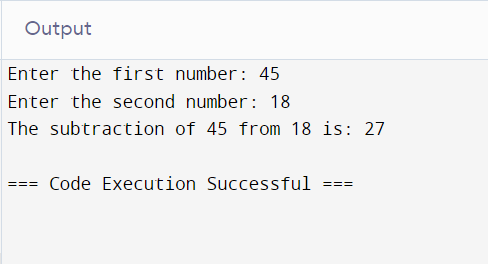
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Using the subtraction operator
result = num1 - num2
# Displaying the result
print(f"The subtraction of {num1} from {num2} is: {result}")
Output:
Multiplication Operator (*)
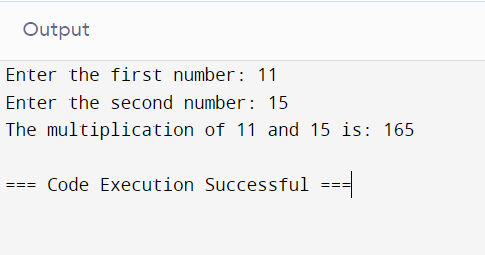
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Using the multiplication operator
result = num1 * num2
# Displaying the result
print(f"The multiplication of {num1} and {num2} is: {result}")
Output:
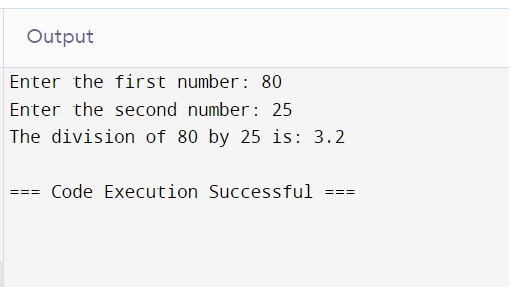
Division Operator (/)
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Using the division operator
result = num1 / num2
# Displaying the result
print(f"The division of {num1} by {num2} is: {result}")
Output:
Modulus Operator (%)
The modulus operator returns the remainder when the first number is divided by the second.
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Using the modulus operator
result = num1 % num2
# Displaying the result
print(f"The modulus of {num1} and {num2} is: {result}")
Output:

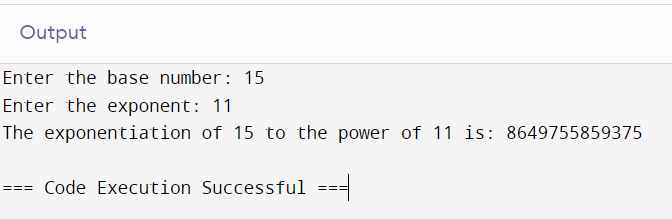
Exponentiation Operator (**)
The exponentiation operator evaluates the first number raised to the power of the second.
# Taking input from the user
base = int(input("Enter the base number: "))
exponent = int(input("Enter the exponent: "))
# Using the exponentiation operator
result = base ** exponent
# Displaying the result
print(f"The exponentiation of {base} to the power of {exponent} is: {result}")
Output:
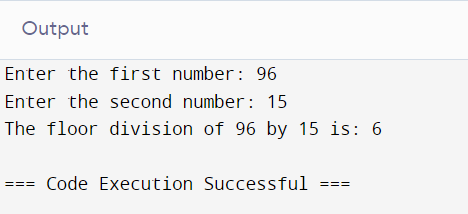
Floor Division Operator (//)
The Floor Division operator divides the first number by the second number, applies the floor division, and returns the nearest whole number result.
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Using the floor division operator
result = num1 // num2
# Displaying the result
print(f"The floor division of {num1} by {num2} is: {result}")
Output:
Handling Mixed Data Types in Arithmetic Operations
Have you ever wondered what happens when we mix different types of numbers in our calculations? Can we add an integer to a float without causing errors?
These are common worries when working with arithmetic operators in Python. Python makes it easy to handle mixed data types in arithmetic operations.
In this case, when addition is performed on two different data types, Python automatically converts the narrower type to the wider type. The process can be illustrated through a simple example:
# Taking input from the user
int_num = int(input("Enter an integer: "))
float_num = float(input("Enter a float: "))
# Performing addition
result = int_num + float_num
# Displaying the result
print(f"The result of adding {int_num} and {float_num} is: {result}")
Output:
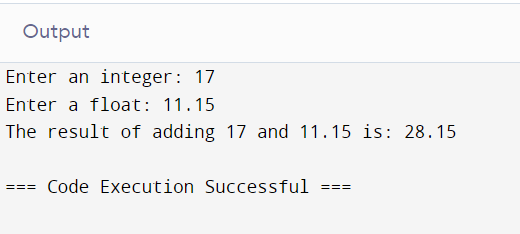
Here, Python converts this integer to a float and then performs the addition; therefore, guaranteeing the accuracy of the answer and eliminating type errors.
The beauty of Python is that it treats mixed data types smoothly and easily. It is a powerful tool with arithmetic operations. We can juggle integers, floats, and even complex numbers in our calculations. That makes one very flexible while writing code—clean and effective.
Here’s another example involving complex numbers:
# Taking input from the user
real_part = float(input("Enter the real part of the complex number: "))
imaginary_part = float(input("Enter the imaginary part of the complex number: "))
# Creating a complex number
complex_num = complex(real_part, imaginary_part)
# Performing addition with an integer
result = complex_num + 5
# Displaying the result
print(f"The result of adding 5 to {complex_num} is: {result}")
Output:

Operations Involving Complex Numbers in Python
Complex numbers may look difficult, but Python handles them very easily. The arithmetic operators in Python perform these operations as easily as working with real numbers. We can operate with them in various ways by using these operators. Here is a quick demonstration with a more operational example:
# Taking input from the user
real1 = float(input("Enter the real part of the first complex number: "))
imag1 = float(input("Enter the imaginary part of the first complex number: "))
real2 = float(input("Enter the real part of the second complex number: "))
imag2 = float(input("Enter the imaginary part of the second complex number: "))
# Creating complex numbers
complex1 = complex(real1, imag1)
complex2 = complex(real2, imag2)
# Performing multiplication
result = complex1 * complex2
# Displaying the result
print(f"The result of multiplying {complex1} and {complex2} is: {result}")
# Performing division
result = complex1 / complex2
# Displaying the result
print(f"The result of dividing {complex1} by {complex2} is: {result}")
Output:


82.9%
of professionals don't believe their degree can help them get ahead at work.
Edge Cases and Exception Handling in Python Arithmetic
Ever tried dividing a number by zero and wondered why your program crashes? Or have you encountered unexpected results when using arithmetic operators in Python?
These are common worries when dealing with edge cases in arithmetic operations. Python provides tools to handle these edge cases effectively.
Division by Zero
One of the most common edge cases is division by zero. Python raises a ZeroDivisionError when we try to divide by zero. We can handle this using a try-except block:
# Taking input from the user
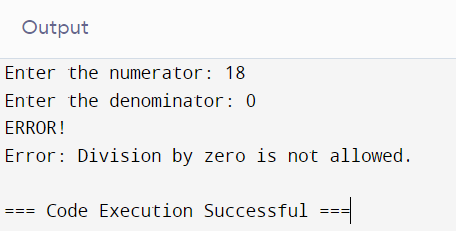
num1 = int(input("Enter the numerator: "))
num2 = int(input("Enter the denominator: "))
# Handling division by zero
try:
result = num1 / num2
print(f"The result of division is: {result}")
except ZeroDivisionError:
print("Error: Division by zero is not allowed.")
Output:
Handling Invalid Inputs
What if a user enters a non-numeric value? We can handle such scenarios using exception handling:
# Taking input from the user
try:
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
# Performing addition
result = num1 + num2
print(f"The addition of {num1} and {num2} is: {result}")
except ValueError:
print("Error: Please enter valid numeric values.")
Output:

Large Numbers and Overflow
Python handles large numbers gracefully, but it’s still good to be cautious.
Here’s an example of handling large numbers:
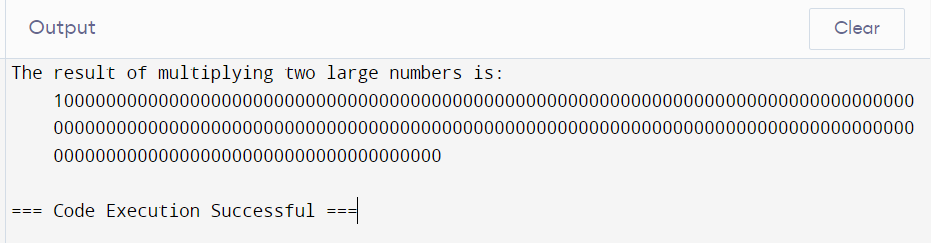
num1 = 10**100 # Very large number
num2 = 10**100
# Performing multiplication
result = num1 * num2
# Displaying the result
print(f"The result of multiplying two large numbers is: {result}")
Output:
Negative Numbers
Negative numbers can also cause unexpected results, especially with division and modulus.
# Taking input from the user
num1 = int(input("Enter a negative number: "))
num2 = int(input("Enter a positive number: "))
# Performing division and modulus
div_result = num1 / num2
mod_result = num1 % num2
# Displaying the results
print(f"The result of division is: {div_result}")
print(f"The result of modulus is: {mod_result}")
Output:

Precedence and Associativity of Python Arithmetic Operators
Since, in some cases, we have to perform more than one operation on the variables within a single problem, it is pertinent to understand the order of operation. Python does this based on the rule of precedence and associativity of the operators.
Precedence of Arithmetic Operators
The precedence of operators determines the order in which different operations are evaluated.
Here is the order of precedence for Python arithmetic operators, from highest to lowest:
- Exponentiation (**)
- Multiplication (*), Division (/), Floor Division (//), and Modulus (%)
- Addition (+) and Subtraction (-)
Associativity of Arithmetic Operators
Associativity is the order of evaluating an expression being operated on by operators of a similar precedence level.
Python arithmetic operators have the following associativity:
- Left to Right: *, /, //, %, +, –
- Right to Left: **
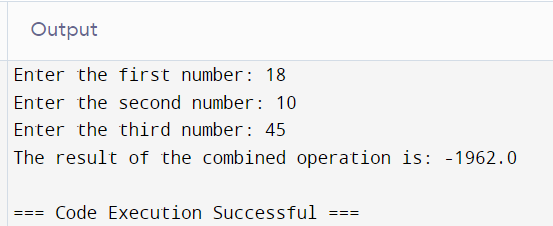
Let’s see an example that combines these rules:
# Taking input from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))
num3 = int(input("Enter the third number: "))
# Performing a combined operation
result = num1 + num2 * num3 / num2 - num3 ** 2
# Displaying the result
print(f"The result of the combined operation is: {result}")Conclusion
Arithmetic operators in Python are the very basic tools we use every day. Mastering them will help us perform a big deal of computations with much ease and accuracy. Be it handling mixed data types, complex numbers, or edge cases, Python’s arithmetic operators make our coding experience smooth and efficient. Keep practising and trying out these operators to continue sharpening your Python skills.
What happens when I divide by zero in Python?
What are Python's basic arithmetic operators?
- Addition (+)
- Subtraction (-)
- Multiplication (*)
- Division (/)
- Modulus (%)
- Exponentiation (**)
- Floor division (//)
How does Python handle arithmetic operations with mixed data types?
Can Python perform arithmetic operations with complex numbers?
Can you explain how the '/' operator is different from '//' in Python?
- ‘/’ operator performs ‘true division’ to yield a float value.
- ‘//’ operator performs ‘floor division’ by giving the end result in integer form, ignoring the fractional part.
Updated on July 27, 2024