Comprehensive Guide to AVL Tree in Data Structure

In the world of data structures, the AVL tree in data structure stands out as a special type of binary search tree (BST) that automatically maintains balance. This balancing act is essential because it ensures that the tree's height remains relatively small, leading to efficient operations like searching, insertion, and deletion. Read all about trees in data structure in detail.

In this guide, we will take you through the AVL tree in data structure, unraveling their secrets and understanding how they work their magic.

What is AVL Trees

AVL tree in data structure is a self-balancing binary search tree in data structures. The name "AVL" comes from their inventors, Adelson-Velsky and Landis. These trees maintain balance by automatically adjusting their structure during insertions and deletions to ensure that the height difference between the left and right subtrees is always limited to -1, 0, or 1. 

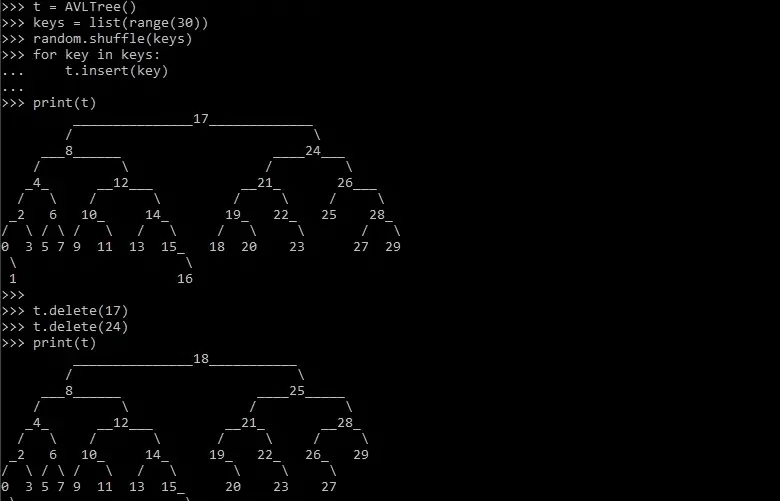
This balanced nature guarantees logarithmic time complexity for operations like search, insert, and delete, making AVL trees highly efficient in managing sorted data. Furthermore, Data visualization tools like D3.js can be used to visualize the AVL tree structure, which makes it easier for developers to debug and understand their code.

Characteristics of AVL Trees

Below are the key characteristics of AVL trees:

• AVL trees are self-balancing binary search trees.
• Each node in an AVL tree has at most two children.
• Any node's height difference between the left and right subtrees (balance factor) is limited to -1, 0, or 1.
• The tree's self-balancing property ensures that the height of the tree remains relatively small.
• This balance guarantees efficient search, insertion, and deletion operations with logarithmic time complexity.

Importance of AVL Trees in Data Structures

The importance of AVL trees in data structures lies in their ability to maintain balance automatically. Maintaining a balanced tree is crucial for efficient operations like searching, inserting, and deleting elements when dealing with large datasets and performing frequent data updates.

By keeping the tree balanced, AVL trees ensure that the height remains relatively small, resulting in consistent and predictable time complexities for various operations. This makes AVL trees ideal for scenarios where quick access to data is vital and performance is critical.

With the self-balancing property of AVL trees, the efficiency of common operations would improve as the tree grows, leading to faster and more reliable algorithms. Hence, AVL trees are fundamental in optimizing data structure operations and improving overall computational efficiency. Data Structures in Java, C++, and other programming languages support AVL trees as a core data structure for their importance in software engineering. 

Benefits of AVL Trees in Data Structures

The benefits of AVL trees in data structures are as follows:

1. Efficient Operations: AVL trees ensure logarithmic time complexity for search, insert, and delete operations. This efficiency remains consistent even as the dataset grows, making them suitable for handling large volumes of data.
2. Self-Balancing: The automatic self-balancing property of AVL trees ensures that the tree's height remains balanced. This results in a more compact tree structure and faster access to data.
3. Predictable Performance: Due to their balanced nature, AVL trees provide predictable and reliable performance for various operations, making them ideal for critical applications.
4. Optimized Searching: AVL trees are designed for efficient searching, which is crucial for applications like databases, where quick access to data is essential.
5. Range Queries: The balanced structure of AVL trees makes them well-suited for range queries, enabling efficient data retrieval within a specified range.
6. Dynamic Data Sets: AVL trees are excellent for scenarios where data is frequently updated, as they maintain balance during insertions and deletions, keeping the tree's performance intact.
7. Versatility: AVL trees can be adapted to various use cases and integrated with other data structures, enhancing their capabilities.
8. Reliable Sorting: AVL trees inherently maintain sorted data, ensuring that elements are always in the correct order, which is advantageous for applications requiring ordered data.
9. Widely Used: AVL trees are a popular choice in computer science and widely used in real-world applications due to their efficiency and reliability.
10. Foundational Data Structure: AVL trees are a foundational data structure in computer science, forming the basis for more complex algorithms and data organization techniques.

Read more about : Threaded Binary Trees

AVL Tree Properties and Operations

Below are the properties and operations of AVL trees:

Properties

• Self-Balancing: The key property of AVL trees is their automatic self-balancing capability. They ensure that the height difference between left and right subtrees of any node is always within the range of -1, 0, or 1, guaranteeing balance.
• Binary Search Tree (BST): AVL trees are a type of binary search tree, meaning each node can have at most two children. The left child contains smaller elements, and the right child contains larger elements than the node.

Operations

• Insertion: When inserting a new element into an AVL tree, it automatically restructures itself to maintain balance. This may involve rotations to adjust the heights of subtrees and preserve the AVL property.
• Deletion: During deletion, the AVL tree maintains balance while removing the specified element. Like insertion, this process may require rotations to maintain the AVL property.
• Searching: Searching in an AVL tree follows the principles of a binary search tree. It quickly narrows the search by comparing the target element with the node's value and recursively moving to the left or right subtree until the target is found.

Maintaining Balance in AVL Trees

Maintaining balance in AVL trees refers to automatically adjusting the tree's structure during insertions and deletions to ensure that the height difference between left and right subtrees remains limited to -1, 0, or 1. This self-balancing property ensures efficient operations and guarantees the tree's logarithmic time complexity.

Applications of AVL Trees

Some key applications of AVL tree include:

1. Database Systems: AVL trees are used to index and organize data in databases, facilitating quick searching and retrieval operations.
2. Language Processing: AVL trees help build language dictionaries and spell-checking systems, efficiently managing word lists.
3. Computer Graphics: AVL trees are applied in computer graphics for collision detection and spatial partitioning.
4. Network Routing: They aid in efficient data routing and managing routing tables in computer networks.
5. Range Queries: AVL trees excel at handling range queries, making them valuable in scenarios where data within specific ranges need to be retrieved quickly.
6. Auto-Complete and Suggestions: AVL trees power auto-complete and suggestion features in search engines and text editors.
7. Symbol Tables: They are utilized in compilers and interpreters to store and manage symbols and their attributes.

Demerits of AVL Tree

Below are some disadvantages of AVL trees:

• The AVL tree's self-balancing mechanism adds complexity to its implementation compared to basic binary search trees.
• Maintaining balance requires additional memory to store balance factors, increasing the memory overhead.
• Frequent insertions and deletions can trigger a series of rotations, impacting performance.
• The balancing process during insertions and deletions can make these operations slightly slower than non-balanced binary search trees.
• The AVL tree's self-balancing might not benefit small datasets significantly, resulting in unnecessary overhead.
• Implementing AVL trees correctly, especially with all the required rotation cases, can be challenging and error-prone.

Conclusion

In this guide we have learned all about AVL trees. The AVL tree in data structure provides efficient and reliable operations through its self-balancing nature. With their ability to maintain a balanced structure, AVL trees ensure fast search, insertion, and deletion operations, making them indispensable for managing large datasets and optimizing algorithms.