10 Types of Programming Languages Every Coder should Know
Learn about different types of programming languages and how they are implemented in the real world.
8 mins read
A queue is a linear structure wherein operations occur in a First In First Out (FIFO) order. Queues are data structures in which the head of the queue is removed in the address space where it was added in the order in which it was received. This principle is useful in organising processes among computer components such as task queuing, process scheduling, and handling. Queues are typically used to manage multithreading threads and implement priority queuing systems.
In this article, we will learn about the types of queues, their application, advantages and disadvantages, and various code examples.
What is Queue in Data Structure?
A queue is a linear data structure that follows the FIFO (First In First Out) method which is open at both ends. In a Queue, elements are added at one end of the ‘rear’ and removed from the other i.e., from the front. In other words, a queue is a collection where deletions are made from the front end of the line, also known as the head of the queue, and insertions are made from the back end, also known as the tail of the queue.
This can be better understood with a real-world example. Suppose you are waiting in line at a ticket counter. The first person in line will be put at the front of the line, and those who arrive later will join the front person from behind. Services will also be provided in that order, so the first person in line will receive their ticket first. This similar kind of approach is followed in a queue data structure.
Key characteristics of a queue:
- Insertion is done at the rear end.
- Deletion is done at the front end.
- The queue grows towards the rear.
POSTGRADUATE PROGRAM IN
Multi Cloud Architecture & DevOps
Master cloud architecture, DevOps practices, and automation to build scalable, resilient systems.
Types of Queue in Data Structure
There are mainly 4 (four) types of Queues in data structures. We will now understand each of them in detail, with their implementation and code examples.
- Simple Queue
- Circular Queue
- Priority Queue
- Double-Ended Queue (Deque)
Simple Queue
The simple queue is the first version of the queue based on the First In First Out (FIFO) principle. Elements are inserted at the rear and removed from the front. However, after performing several insertions and deletions, such a class for the queue can also offer many downsides because of the empty spaces witnessed after some elements are dequeued.
The front end of the queue is the location where the deletion occurs, and the rear end is the location where the insertion occurs. It is used in situations where data consumption should occur in a first-in, first-out (FIFO) principle, but where there may be a requirement to discard recently added data owing to performance concerns or irrelevant data. It should be noted that to remove a newly added element, all items that were added previously must be removed. A simple queue is also known as the Input Restricted Queue.
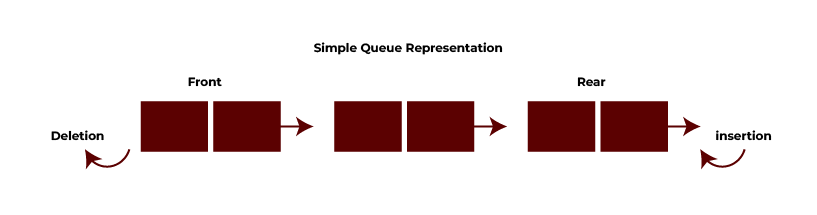
Implementation
An array or linked list is used to build the Simple Queue (also a Linear Queue). Two important rules to remember are:
- front: The first piece in the queue is tracked by this pointer.
- rear: The last piece in the queue is tracked by this pointer.
Operations of Simple Queue:
Below are the operations of a simple queue in data structure:
- Enqueue: The new element is added at the location that the rear pointer points to, and the rear pointer is incremented. If the queue is full (i.e., the rear is at the last index of the array), it can either return an overflow error or reallocate memory. The time complexity for this operation is O(1).
- Dequeue: The element at the position pointed to by the front is removed, and the front pointer is incremented. An underflow error is returned if the queue is empty, meaning that both the front and back are at zero. The time complexity for this operation is O(1).
- Peek: Returns the element at the front without removing it. The time complexity for this operation is O(1).
Code Example:
C++
#include <iostream>
using namespace std;
#define SIZE 5 // Define the maximum size of the queue
class SimpleQue {
private:
int items[SIZE]; // Array to store queue elements
int front, rear; // Pointers to manage the front and rear of the queue
public:
SimpleQue() {
front = -1; // Initialize front to -1 (empty state)
rear = -1; // Initialize rear to -1 (empty state)
}
// Function to check if the queue is full
bool isFull() {
return rear == SIZE - 1; // Queue is full when rear reaches the last index
}
// Function to check if the queue is empty
bool isEmpty() {
return front == -1; // Queue is empty when front is -1
}
// Enqueue operation to add an element to the queue
void enqueue(int element) {
if (isFull()) {
cout << "Queue is full\n";
} else {
if (front == -1) front = 0; // If inserting the first element, set front to 0
rear++;
items[rear] = element; // Insert element at the rear
cout << "Inserted: " << element << endl;
}
}
// Dequeue operation to remove an element from the queue
int dequeue() {
int element;
if (isEmpty()) {
cout << "Queue is empty\n";
return (-1);
} else {
element = items[front];
if (front >= rear) {
// If only one element was in the queue
front = -1;
rear = -1;
} else {
front++; // Move front pointer forward
}
cout << "Removed: " << element << endl;
return element;
}
}
// Peek operation to see the element at the front without removing it
int peek() {
if (isEmpty()) {
cout << "Queue is empty\n";
return (-1);
} else {
return items[front]; // Return front element
}
}
// Display the queue elements
void display() {
if (isEmpty()) {
cout << "Queue is empty\n";
} else {
cout << "Queue elements: ";
for (int i = front; i <= rear; i++)
cout << items[i] << " ";
cout << endl;
}
}
};
int main() {
SimpleQue q;
q.enqueue(102);
q.enqueue(104);
q.enqueue(106);
q.enqueue(108);
q.display(); // Display all elements
q.dequeue(); // Remove element from the queue
q.display();
q.enqueue(110); // Attempt to enqueue another element
q.display();
cout << "Peek: " << q.peek() << endl; // Peek at the front element
return 0;
}
Output:
Inserted: 102
Inserted: 104
Inserted: 106
Inserted: 108
Queue elements: 102 104 106 108
Removed: 102
Queue elements: 104 106 108
Inserted: 110
Queue elements: 104 106 108 110
Peek: 104
Applications:
- Job Scheduling: A queue is established and the processes or jobs are processed in the order in which they are received within that queue. The processes would be connected into a queue which is followed till sequential execution is complete.
- Disk Scheduling: The requests to use the disk are kept in a queue and addressed one after the other as if they were events that had been waited for.
- Call Centre System: Customer service queuing strategies are basic in a manner that customers that call are serviced in the order in which they are called.
- Printer Task Management: Whenever any number of print jobs are sent to the printer, they are managed using a basic FIFO queue whereby the first job that goes in is the first one that comes out.
- Shared Resources in Networks: Whenever packet buffering is required in a computer network there is always a first-in first-out buffer used. All packets are received and sent out in turn till each one has been sent out.
Circular Queue
A circular queue is an advancement on the simple queue. In a circular queue, all the nodes are connected circularly. Here, the last position is joined to the first position forming a circular shape. This elimination solves the problem of empty spaces found in simple queues after enqueuing and dequeuing several times.
A circular queue is also known as a ring buffer because all of the ends are connected. A circular queue stores its elements in a circular buffer. A circular queue also solves the issue of overflow in a simple queue and offers an effective way to manage memory that is constrained. Circular queues are used in a variety of disciplines, including memory management, CPU scheduling, etc., because of their efficient operation and ability to manage data cyclically.
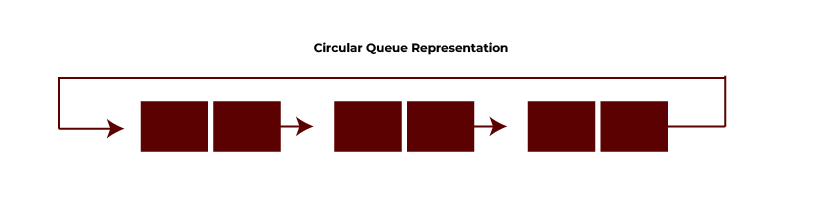
Implementation
The problem of wasted space in a linear queue is solved by a circular queue data structure. After elements are dequeued, the space is reused using a circular array.
- front: Indicates which element is at the front of the line.
- back: Indicates the final item in the line.
Logic:
- Using modulo arithmetic, the front and rear pointers wrap around as (front + 1) % SIZE and (rear + 1) % SIZE, respectively.
- This guarantees that even after dequeuing elements, the queue can effectively use the entire array size.
Operations of Circular Queue:
Below are the operations of a Circular queue in data structure:
- Enqueue: The rear pointer is incremented using (rear + 1) % SIZE, and the new element is added at this position. The time complexity for this operation is O(1).
- Dequeue: The front pointer is incremented using (front + 1) % SIZE, and the element is removed from this position. The time complexity for this operation is O(1).
- Peek: Returns the element at the front without removing it. The time complexity for this operation is O(1).
Code Example:
C++
#include <iostream>
using namespace std;
#define SIZE 5 // Define the size of the circular queue
class CircularQue {
private:
int items[SIZE]; // Array to store queue elements
int front, rear; // Front and rear pointers
public:
CircularQue() {
front = -1;
rear = -1;
}
// Check if the queue is full
bool isFull() {
return (front == 0 && rear == SIZE - 1) || (front == rear + 1);
}
// Check if the queue is empty
bool isEmpty() {
return front == -1;
}
// Enqueue operation
void enqueue(int element) {
if (isFull()) {
cout << "Queue is full\n";
} else {
if (front == -1) front = 0; // If first element, set front to 0
rear = (rear + 1) % SIZE; // Circular increment
items[rear] = element;
cout << "Inserted: " << element << endl;
}
}
// Dequeue operation
int dequeue() {
int element;
if (isEmpty()) {
cout << "Queue is empty\n";
return -1;
} else {
element = items[front];
if (front == rear) {
// Queue has only one element, reset queue
front = -1;
rear = -1;
} else {
front = (front + 1) % SIZE; // Circular increment
}
cout << "Removed: " << element << endl;
return element;
}
}
// Peek operation
int peek() {
if (isEmpty()) {
cout << "Queue is empty\n";
return -1;
} else {
return items[front];
}
}
// Display the queue elements
void display() {
if (isEmpty()) {
cout << "Queue is empty\n";
} else {
cout << "Queue elements: ";
int i = front;
while (i != rear) {
cout << items[i] << " ";
i = (i + 1) % SIZE;
}
cout << items[rear] << endl; // Print the last element
}
}
};
int main() {
CircularQue q;
q.enqueue(102);
q.enqueue(104);
q.enqueue(106);
q.enqueue(108);
q.enqueue(110); // Queue becomes full here
q.display(); // Display all elements
q.dequeue(); // Remove one element
q.display();
q.enqueue(120); // Insert a new element
q.display();
return 0;
}
Output:
Inserted: 102
Inserted: 104
Inserted: 106
Inserted: 108
Inserted: 110
Queue elements: 102 104 106 108 110
Removed: 102
Queue elements: 104 106 108 110
Inserted: 120
Queue elements: 104 106 108 110 120
Applications:
- Memory Management: Circular queues come to use when there is a need to implement fixed memory buffers, like buffers in low-level device drivers where data continuously needs to be written and read cyclically.
- Traffic Light System: In cases of traffic light management especially in an intersection the next lane to serve is chosen from a circular queue whereas every road is attended to in turn.
- Multiplayer Game: Players in multiplayer games who take turns in a sequential order are controlled by circular queues as the turn of each player comes in a fixed sequence.
Priority Queue
A priority queue is a form of queue in which each element is assigned a priority and dequeued based on that priority rather than the order of input. Higher-priority elements are dequeued first, and vice versa. In simpler words, the node with the lowest priority will be the first removed from the queue. The insertion occurs in the order in which the nodes arrive.
This makes it valuable in a variety of real-world applications, including operating system process scheduling, graph theory’s shortest-path algorithms (Dijkstra’s, etc), and event-driven simulations.
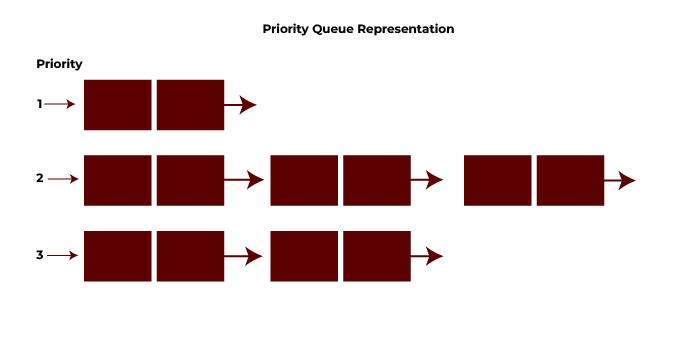
Implementation
A binary heap, linked list, or array is used to implement the priority queue. A min-heap or max-heap is the most effective technique (for high-priority pieces at the top).
Priority Management Logic:
- Every element has a priority, and when an element is inserted, it always dequeues the element with the highest priority first.
- To put elements in the proper place in an array-based implementation, sorting or linear search are used.
- Large datasets are better served by heaps since the element with the highest priority can be retrieved in O(log n) time.
Operations of Priority Queue:
Below are the operations of a Priority queue in data structure:
- Enqueue: Elements are added by their priority.
- This can entail sorting in an array or linked list.
- This operation can be completed in O(log n) in a heap. The time complexity for this operation is O(log n) for heaps and O(n) for sorted arrays or lists.
- Dequeue: The element with the highest priority is eliminated, based on the implementation. The time complexity for this operation is O(log n) for heaps and O(n) for sorted arrays or lists.
- Peek: Returns the element with the highest priority without removing it. The time complexity for this operation is O(1).
Code Example:
C++
#include <iostream>
#include <vector>
#include <bits/stdc++.h>
using namespace std;
class PriorityQueue {
private:
vector<int> pq; // Dynamic array to store elements
public:
// Insert an element based on priority
void enqueue(int element) {
pq.push_back(element); // Insert the element at the end
sort(pq.begin(), pq.end());
cout << "Inserted: " << element << endl;
}
// Dequeue the max-priority element
int dequeue() {
if (pq.empty()) {
cout << "Queue is empty\n";
return -1;
} else {
int element = pq.front(); // Element with the highest priority
pq.erase(pq.begin()); // Remove the front element
cout << "Removed: " << element << endl;
return element;
}
}
// Peek operation to return the max-priority element without removing it
int peek() {
if (pq.empty()) {
cout << "Queue is empty\n";
return -1;
} else {
return pq.front();
}
}
// Display the queue elements
void display() {
if (pq.empty()) {
cout << "Queue is empty\n";
} else {
cout << "Queue elements: ";
for (int i = 0; i < pq.size(); i++)
cout << pq[i] << " ";
cout << endl;
}
}
};
int main() {
PriorityQueue pq;
pq.enqueue(300);
pq.enqueue(100);
pq.enqueue(200);
pq.display(); // Display all elements (sorted)
pq.dequeue(); // Remove the max-priority element (smallest will be returned)
pq.display();
return 0;
}
Output:
Inserted: 300
Inserted: 100
Inserted: 200
Queue elements: 100 200 300
Removed: 100
Queue elements: 200 300
Applications:
- Dijkstra’s Shortest Path Algorithm: Priority queues help in finding the shortest path between nodes in a graph. This is achieved by first selecting the nodes which, according to the algorithm, have the smallest path weight.
- Process Prioritisation: In some operating systems, the processes are given priorities, and a process is selected by the scheduler for which the highest priority is to be executed.
- Huffman Coding: In the Huffman coding algorithm, the priority queues select the two least frequent characters for encoding.
- Event-Driven Simulations: In event-driven simulations, priority queues are used to make sure that events are being processed in timing or priority order.
Double-Ended Queue (Deque)
A double-ended queue (Deque) is a type of queue that permits insertion and deletion from both the front and back ends. A deque can support both FIFO (First In First Out) and LIFO (Last In First Out) operations, and therefore we may call this a cross between a stack and a queue. A deque is a flexible data structure that enables effective insertion and deletion at both the front and the end of the queue. This provides more versatility than a standard queue. The Deque can be further divided into two unique queues: input-restricted and output-restricted.
- Input-restricted deque: In an imputed-restricted deque, insertion operations can only be performed at one end, whereas deletion operations can be performed from both ends.
- Output-restricted deque: In an output-restricted deque, deletions can only be performed at one end, while insertions can be performed at both. It is the opposite of input-restricted deque.
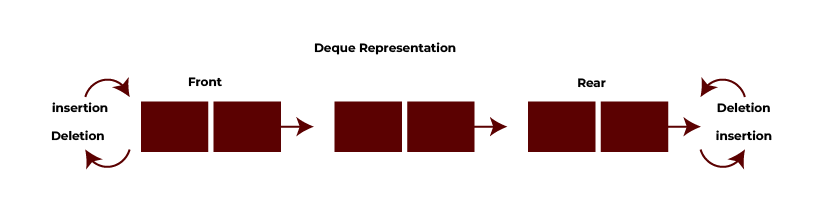
Implementation
The Deque is implemented as a circular array or linked list, allowing insertion and deletion from both the front and the rear. Two important rules to remember are:
- front: Points to the first element of the deque.
- rear: Points to the last element of the deque.
Operations of Deque:
Below are the operations of a Deque in data structure:
- Insert at Front: Decreases the front pointer (wrap around with modulo arithmetic for circular arrays) and adds the element. The time complexity for this operation is O(1).
- Insert at Rear: Increases the rear pointer and adds the element. The time complexity for this operation is O(1).
- Delete from Front: Removes the element at the front pointer and modifies it appropriately. The time complexity for this operation is O(1).
- Delete from Rear: Removes the element at the rear pointer and modifies it appropriately. The time complexity for this operation is O(1).
- Peek: Returns the element at either end. The time complexity for this operation is O(1).
Code Example:
C++
#include <iostream>
using namespace std;
#define SIZE 5 // Define the size of the deque
class Deque {
private:
int items[SIZE]; // Array to store deque elements
int front, rear; // Pointers for the front and rear of the deque
public:
Deque() {
front = -1;
rear = -1;
}
// Check if the deque is full
bool isFull() {
return (front == 0 && rear == SIZE - 1) || (front == rear + 1);
}
// Check if the deque is empty
bool isEmpty() {
return front == -1;
}
// Insert at the front
void insertFront(int element) {
if (isFull()) {
cout << "Deque is full\n";
} else {
if (front == -1) { // Inserting the first element
front = 0;
rear = 0;
} else if (front == 0) {
front = SIZE - 1; // Wrap around to the end
} else {
front--;
}
items[front] = element;
cout << "Inserted at front: " << element << endl;
}
}
// Insert at the rear
void insertRear(int element) {
if (isFull()) {
cout << "Deque is full\n";
} else {
if (front == -1) { // Inserting the first element
front = 0;
rear = 0;
} else if (rear == SIZE - 1) {
rear = 0; // Wrap around to the front
} else {
rear++;
}
items[rear] = element;
cout << "Inserted at rear: " << element << endl;
}
}
// Remove from the front
int delFront() {
if (isEmpty()) {
cout << "Deque is empty\n";
return -1;
} else {
int element = items[front];
if (front == rear) {
front = -1;
rear = -1; // Reset deque
} else if (front == SIZE - 1) {
front = 0; // Wrap around to the front
} else {
front++;
}
cout << "Removed from front: " << element << endl;
return element;
}
}
// Remove from the rear
int delRear() {
if (isEmpty()) {
cout << "Deque is empty\n";
return -1;
} else {
int element = items[rear];
if (front == rear) {
front = -1;
rear = -1; // Reset deque
} else if (rear == 0) {
rear = SIZE - 1; // Wrap around to the end
} else {
rear--;
}
cout << "Removed from rear: " << element << endl;
return element;
}
}
// Display the deque elements
void display() {
if (isEmpty()) {
cout << "Deque is empty\n";
} else {
cout << "Deque elements: ";
int i = front;
while (i != rear) {
cout << items[i] << " ";
i = (i + 1) % SIZE;
}
cout << items[rear] << endl; // Print the last element
}
}
};
int main() {
Deque dq;
dq.insertRear(10);
dq.insertRear(20);
dq.insertFront(30);
dq.insertFront(40);
dq.display(); // Display all elements
dq.delFront(); // Remove from front
dq.delRear(); // Remove from rear
dq.display();
return 0;
}
Output:
Inserted at rear: 10
Inserted at rear: 20
Inserted at front: 30
Inserted at front: 40
Deque elements: 40 30 10 20
Removed from front: 40
Removed from rear: 20
Deque elements: 30 10
Applications:
- Task Scheduling: Deques offers flexibility to handle jobs in multiple orders in task management systems because tasks may have priorities that allow them to be addressed from either the front or the back.
- Palindrome Checking: A deque can check whether a string is a palindrome by simultaneously reading the characters of the string from both ends.
- Undo Operations in Applications: Deques are a data structure primarily used in implementing undo functionality in applications like text editors supporting operations where we need to access both ends of history (most recent actions and oldest actions).
Advantages of Queue in Data Structure
- FIFO Order
One primary advantage of a queue is that it can realise FIFO. That is, the first in time to be added is the first to be removed. This is of importance in actual real-world systems such as scheduling, buffering, and task management.
- Efficient Task Scheduling
Queues are used in all task scheduling systems to manage processes. CPU scheduling algorithms such as First-Come-First-Serve use queues to fairly implement efficient process execution.
- Shared Resource Management
Queues are perfect when managing shared resources. In networking, queues help in data packet handling to maintain the order of carry and forward.
- Asynchronous Data Transfer
Queues are most heavily implemented in IPC for buffering. That is if the producer is creating data at a different rate than the consumer can handle, it allows asynchronous data exchange by temporarily storing the message.
- Memory Efficiency in Circular Queues
Circular queues are an optimization over memory usage. They have no problem with the waste of space, as in the case of a simple linear queue. Once elements have been dequeued from the queue, their positions can be used again in a circular fashion.
- Supports Parallelism
In distributed systems or parallel processing, for example, the queuing discipline, queues hold the tasks in them so that these will be guaranteed to be processed in the order of arrival. It helps with load balancing and proper utilisation of system resources.
Disadvantages of Queue in Data Structure
- Queue overflow and underflow
In array-based implementations where the size is fixed, queues may overflow when they reach capacity. Underflow may also happen when you try to dequeue from an empty queue. The implementation process needs to handle these problems properly.
- Slow Search and Access
In contrast to data structures such as arrays or trees, searching for an element in a queue is slow since elements cannot be accessed directly. Dequeuing elements one at a time is necessary to locate an item, which renders the technique ineffective for searches or random access operations.
- Deadlocks
When several threads or processes are waiting on one another to release resources, a deadlock happens and none of the threads can move forward.
- Complex Implementation for Priority Queue
Priority queues, while efficient for tasks that require different priorities for elements, have more complex insertion and deletion operations (especially if implemented with a heap). Maintaining the correct order for priority in every insertion adds extra time and space complexity compared to a basic queue.
82.9%
of professionals don't believe their degree can help them get ahead at work.
Conclusion
Queues are a fundamental concept in data structures, and they are of various types and have different use cases in different scenarios. We have covered majorly 4 types of queues in this article, along with each of their implementation, applications, code implementations, etc. Simple queues are suitable for basic FIFO operations, circular queues address memory wastage, priority queues offer task prioritisation, and deques provide flexibility with double-ended operations.
Understanding these different types of queues, along with their implementation, is crucial for solving real-world problems efficiently. Different applications are there for each type of queue, and having a deep knowledge of each type will help you apply the best queue data structure in your next application.
FAQs
What are the types of queues in C++?
There are various types of queues in C++ such as simpler queues, circular queues, priority queues, and double-ended queues (Deque). These different types of queues can be implemented using various data structures such as arrays, linked lists, or heaps, depending on the requirements.
What is the difference between a priority queue and a double-ended queue?
Priority Queue and Deque serve different but essential functions within the data elements’ organisation. A priority queue is defined as one that orders its elements not according to the order in which they were inserted but rather on the order in which they are likely to be dequeued. A Deque on the other hand accepts elements and removes elements from both sides i.e., front end and rear end, but there is no order of importance amongst the elements.
What is a priority queue and its types?
A priority queue is a type of queue in which the elements are inserted or removed according to their priorities. There are two types of priority queues: Min-Priority Queue and Max-Priority Queue. In a Min-Priority Queue, the first element to be removed is the element that has the least priority and in a Max-Priority Queue, the first element to be removed is the one with the highest.
Can deadlock occur in the queue data structure?
It can’t be determined straightly that deadlock can occur in the queue data structure. However, it has been shown that they can lead to the creation of deadlocks, especially in systems designed with queue-based communication or resource management like the OS or the multithreaded environment. If two or more processes are in waiting states on each other to release resources held in a queue then a deadlock may occur.
Are there any synchronisation issues in the queue data structure?
Yes, when many threads are concurrently using the same queue, synchronisation problems may occur. Errors like race conditions and data corruption may arise from the synchronisation issues.
Updated on October 9, 2024
Link
