Spanning Tree in Data Structure: Algorithms, Applications & More

Have you ever wondered how your GPS finds the shortest route or how data packets can travel efficiently across networks? These systems rely on the spanning tree data structure to improve paths. Spanning trees not only mitigate errors within complex computer networks but also support the infrastructure of telecommunication networks to sensibly uphold the pace of efficient operations. In this article, we will look at what a spanning tree is in data structure, along with its functionalities and applications.

Understanding Graphs and Their Types

Undirected Graph

A graph is said to be undirected when all the edges of that graph are bidirectional (not unidirectional); that is, it doesn’t point to a specific direction and has both. We can also define it as a graph of V vertices and E edges in which two vertices are connected.

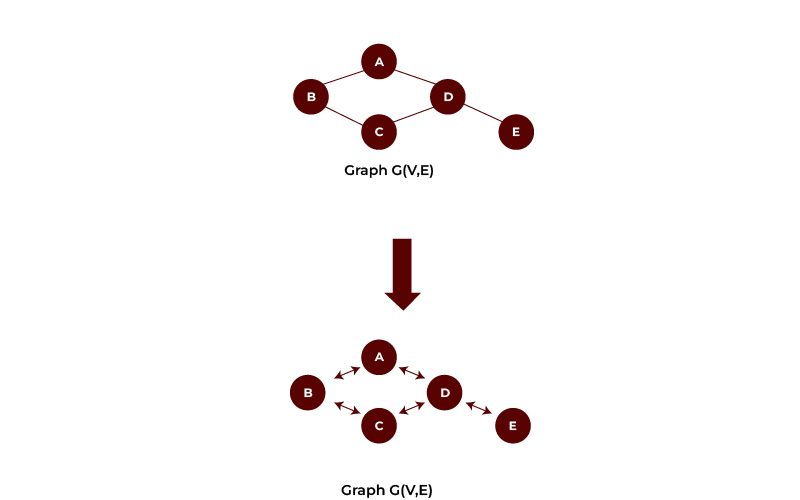
Directed Graph

Such graphs are also called directed graphs or digraphs. A directed graph (or simply digraph) is a graph where, for every pair of vertices, there is at most one edge between them, and any edge can universally have a head in the first vertex and a tail in the second vertex.

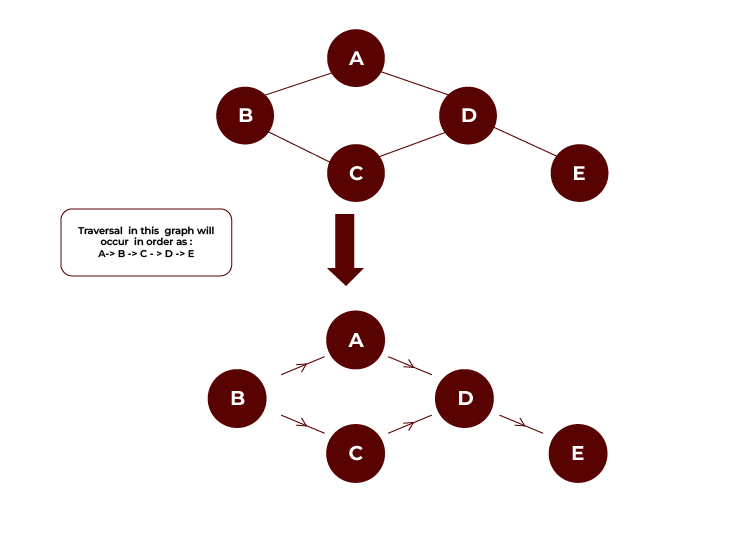
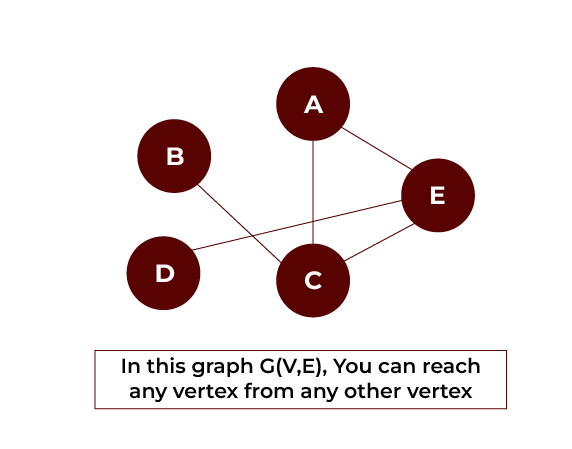
Connected Graph

In a connected graph, a path always exists from one vertex to another. A graph is connected if we can get to any vertex from any other vertex along edges in either direction.

Also Read: Graphs in Data Structures

The spanning tree is a subgraph of an undirected connected graph. It is the subset of vertices in the subgraph such that their sum is the least number of edges, which will connect every vertex (with no loop or cycle forming).

A given graph must have an equal number of vertices as a spanning tree. We have n-1 number of edges in the spanning tree. The number n of vertices in the graph is used here. But the edges of the spanning tree may or may not weigh with them. It depends if the graph itself has weight edges or not.

Minimum Spanning Tree

The minimum spanning tree is a way to connect all the points (or nodes) in a weighted graph using the smallest possible weight total to connect (or edges). It ensures all the points are connected without forming any loops using the least possible weight or cost they need. Building efficient networks — such as laying out cables or planning roads — is where MSTs can come into play to save on resources and cut costs.

Algorithms for Minimum spanning tree

Prim’s Algorithm

The gist is that Prim’s algorithm finds a minimum spanning tree (MST) of a graph subject to the initial choice of our initial vertex from which to start. The algorithm progresses as follows:

• Begin with a random vertex.
• Connect the tree to new vertices by adding edges with the lowest weight.
• Go on until all vertices are involved.

The pseudocode creates two sets: There is U, which contains visited vertices, and V−U, consisting of the remaining unvisited ones. The edges from V−U to U are created with the lowest weight added. Here’s a simplified pseudocode:

• The initial Universe is {1} and the empty tree T.
• While U!=V, add the lowest cost edge between U and (V−U).

It can be implemented for efficiency using adjacency matrices or adjacency lists. Its time complexity is

O(V² ). Applications include network design, electrical wiring layout, and the design or creation of network protocols. Unlike Kruskal’s algorithm, where it starts from a vertex and adds adjacent edges, Prim begins from a vertex and then grows by adding the edges connected to it, and we avoid cycles.

Kruskal’s Algorithm

We can use Kruskal’s algorithm to get a minimum spanning tree (MST) of a graph by selecting the smallest weights edges that do not form a cycle. The steps consist of sorting the edges by weight, adding the lowest weight edge, and repeating until all vertices are covered but avoiding cycles. The method uses the Union Find to check for cycles by clustering vertices. Here’s a pseudocode outline:

• Start with an empty set.
• Sort edges and make sets for each vertex.
• Add edges if they don’t form a cycle using the UNION and FIND operations.

The algorithm requires O(E log E) time. It applies to electrical wiring layouts, insulators, optical fiber networks, and LAN connections. Its use is shown in Java, Python, and C/C++ implementations. Prim’s algorithm differs from Kruskal’s in each case. They both start at a vertex; they add edges to the MST connected directly in each case.

Also Read: Graph Traversal in Data Structure

Properties of Spanning Tree

When we think about trees over a graph, G, spanning trees have special properties. Let’s go over some of the essential characteristics:

• Multiple Spanning Trees: An example of such a connected graph is a spanning tree of G, which can be many spanning trees. All give alternative ways of connecting all vertices without making loops.

• Consistent Edges and Vertices: Each spanning tree is from the same graph ‘G’ and is guaranteed to have the same number of edges and vertices, which is uniform.

• Cycle-Free Structure: A spanning tree is an acyclic G subgraph with no cycles or loops. The value of this property leads each vertex to be connected without a closed loop.

• Minimally Connected: One edge removed from the spanning tree makes it disconnected. This tree’s minimal connectivity demonstrates its efficiency at the basic level of connection.

• Maximally Acyclic: A cycle is formed when adding another edge, which makes the spanning tree and, therefore, becomes a circuit. It shows that the spanning tree is the most reduced form of acyclic structure.

Applications of Spanning Tree

Spanning trees are applied in various fields:

• Computer Network Routing: Managing and organizing networks across data requires spanning trees so data can travel efficiently. These trees make networks such as LAN and WAN run smoothly, help prevent loops, and find the shortest and most efficient routes data packets take to travel.

• Cluster Analysis: Spanning trees form clusters or group-related data points. This makes finding patterns, connections, or trends in vast amounts of data easier, particularly in statistics and machine learning.

• Civil Network Planning: Spawning trees optimize infrastructure designs such as roads, pipelines, and electrical grids. Finding the best routes by minimizing costs and using resources efficiently improves network performance and reliability.

Also Read: Data Structure Interview Questions and Their Answers

Conclusion

Data structures spanned by trees are fundamental; their presence frequently optimizes a network or secures fast connections. They provide the simplest way to maintain connectivity in a graph by eliminating cycles and reducing the number of edges. In computer science and other disciplines, spanning trees are used everywhere, from computer network routing to civil infrastructure planning, and hence, they are so important. Understanding their properties and applications improves our knowledge of data structures and paves the way to solving these real-world problems efficiently. If you are ready to advance in your coding career, apply for the Hero Vired Integrated Program in Data Science, Artificial Intelligence, & Machine Learning, which is offered in collaboration with MIT Open Learning.