Selection Sort is a simple comparison-based sorting algorithm that repeatedly finds the minimum element from the unsorted portion of an array and moves it to the beginning. It is easy to implement and works well for small datasets, though it is not as efficient for large datasets due to its O(n2)O(n^2)O(n2) time complexity.
What is the Selection Sort?
The selection sort is a straightforward sorting algorithm that works by repeatedly selecting the smallest (or largest, depending on the desired order) element from an unsorted portion of the list and moving it to the beginning (or end) of the sorted portion.
Selection sorts divide the list into two sublists.
Sorted sublists: These are built on the left end of the list from left to right.
Unsorted sublist: That is the rest of the unsorted list on the right end.
Get curriculum highlights, career paths, industry insights and accelerate your technology journey.
Download brochure
Flowchart of the Selection Sort
Let’s describe the selection sort algorithm flowchart that could be followed like this.
Start: Begin the process.
Input List: Obtain the list of array elements that will be sorted.
Initialize: It is the current index at the starting index. This represents the beginning of the unsorted portion of the list.
Find Minimum: It traverses the rest of the unsorted portion to find the smallest element.
Swap: It is the smallest element found in the current index.
Increment Index: This increases the current index by one, moving the boundary of the sorted and unsorted portions of the list.
Check: Check if the current index is less than the length of the list -1. If it is, go back to the “Find Minimum” step. If not, all elements have been sorted.
End: End the process. The list is now sorted in ascending order.
How Does Selection Sort Work?
Let’s see how selection sorts work. Arrange the students in height-wise order. In that case, we can follow these steps to arrange the students in height-wise order.
First, divide the queue of students into two parts – arranged and unarranged.
To begin with, place all the students in the unarranged queue.
In this unarranged queue, search for the shortest student and place him/her in the arranged student list.
Again, we had to rearrange the queue and select the second-shortest student. This placed the student in the arranged queue just after the smallest student.
Repeat the above steps until all the students are placed into the arranged queue.
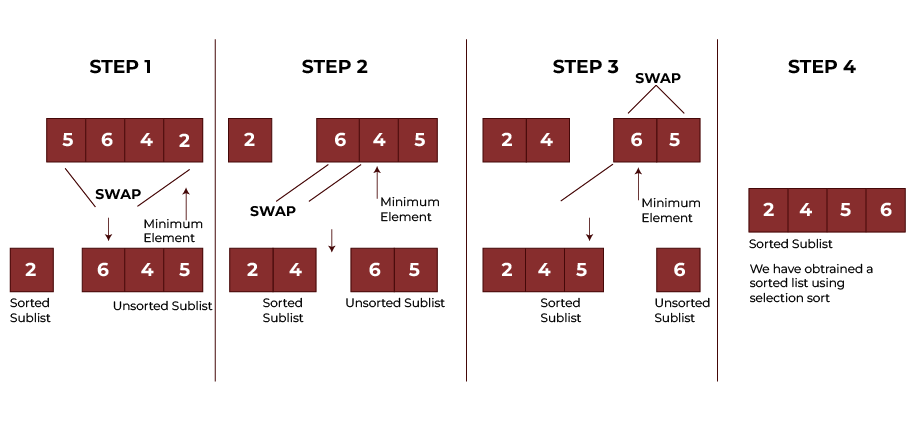
Let’s consider that we want to sort a list in ascending order. Follow the following algorithm.
Start from the first element. At this point, the entire list is unsorted. And the sorted sublist is empty.
Iterate over the list to search for the smallest element in the list.
Add this element to the sorted sublist and remove it from the unsorted sublist. In other words, swap the smallest element in the unsorted sublist with the element that is present at its correctly sorted position.
Repeat this process until all the elements from the unsorted sublists are transferred to the sorted sublists.
Selection Sort Algorithm
We know that to sort a list of n elements using selection sort. We need to perform n-1 iterations.
begin selectionSort(list)
for i = 0 to sizeof(list) - 1
minIndex = i;
for j = i + 1 to sizeof(list)
if list[j] < list[mid_index]
minIndex = j;
end if
swap(list[minIndex], list[i])
end for
end for
end selectionSort
Run the loop from i =0 till the size of the list under the loop.
Declare a variable called minIndex. minIndex helps track the index of the next element that will be swapped with the element at the index i.
Run a nested for loop with j =i+1 until the list size. We initialise j with i+1 since it allows us to reduce the total number of comparisons made under this loop.
Check if the element at the index j is smaller than at the index mid_index. If it is, set minIndex equal to j. It helps us search for the smallest element in the unsorted sublist
Swap the element at index i with the element at index minIndex. This allows us to place the smallest element from the unsorted sublist at the end of the sorted sublist. We update the value of minIndex each time we find an element smaller than it.
Selection Sort Code
Selection Sort Code in Java
class SelectionSort{
static void selectionSort(int arr[]){
int size = arr.length;
for (int i = 0; i < size - 1; i++){
int minIndex = i;
for (int j = i+1; j < size; j++)
if (arr[j] < arr[minIndex])
minIndex = j;
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
public static void main(String args[]){
int arr[] = {33,44,55,99,34} ;
selectionSort(arr) ;
for(int i =0;i<arr.length;i++){
System.out.print(arr[i]+" ") ;
}
System.out.println();
}
}
Output
33 34 44 55 99
2. Selection Sort Code in Python
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_index = i
for j in range(i + 1, n):
if arr[j] < arr[min_index]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
array = [64, 25, 12, 22, 11]
selection_sort(array)
print("Sorted array:", array)
Output
Sorted array: [11, 12, 22, 25, 64]
3. Selection Sort Code in C++
#include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
int main() {
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr) / sizeof(arr[0]);
selectionSort(arr, n);
cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
Output
Sorted array: 11 12 22 25 64
4. Selection Sort in JavaScript
function selectionSort(arr) {
let n = arr.length;
for (let i = 0; i < n - 1; i++) {
let minIndex = i;
for (let j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
let temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
// Example usage
let array = [64, 25, 12, 22, 11];
selectionSort(array);
console.log("Sorted array:", array);
Output
Sorted array: [ 11, 12, 22, 25, 64 ]
Complexity Analysis of Selection Sort
Time Complexity: Selection Sort time complexity with this.
Worst Case O(n2): The worst case occurs when we want to sort a list in ascending order. But it is arranged in descending order.
Average Case: O(n2): The average case is when the list is arranged in a jumbled order.
Best Case: O(n): The best case occurs when the list is already arranged in the desired order. It recalls the part where we concluded to sort a list of n elements.
Space Complexity
The space complexity of the selection sort algorithm is O(1).
Selection Sort is an efficient sorting algorithm for checking if all elements are already sorted. This means it can quickly confirm a sorted list.
It is useful for small arrays or datasets, where its inefficiencies are not very noticeable.
Selection Sort is one of the simplest sorting algorithms, which makes it easy to understand and implement.
Applications of Selection Sort
Selection Sort is good for teaching the fundamentals of sorting mechanisms and algorithm design.
It is suitable for small lists where the overhead of more complex algorithms isn’t justified.
It is ideal for systems with limited memory due to its in-place sorting capability.
Selection sort is used in simple embedded systems where resource availability is limited and simplicity is important.
Conclusion
In this context, we were able to discuss the selection sort. Unix sort is actually a very simple sorting algorithm that works step by step, at each iteration, sequentially, to identify the least or greatest from the element in each sorting array and move it to the sorted array. The time complexity is about o(n2); thus, it is quite slow compared to other algorithms, such as Quick Sort or Merge Sort, which are easy to program.
FAQs
When should I use Selection Sort?
The selection sort operates in place and is best used for small lists or when memory space is a concern. It is also a good educational tool for understanding sorting concepts, but for larger datasets, more efficient algorithms like Quick Sort or Merge Sort are recommended.
Can Selection Sort be used on linked lists?
Yes, Selection sort can be implemented on linked lists, but the efficiency may vary compared to arrays due to the different access patterns. The swapping mechanism will also be different since you cannot directly swap nodes as you do with array elements.
What is the space complexity of Selection Sort?
The space complexity of the selection sort is O(1) because it only requires a constant amount of additional space for variables used in the sorting process, making it memory efficient.
Is it possible to implement Selection Sort without using any loops?
We can implement a recursive version of Selection Sort that does not use explicit loops, though it may be less efficient and harder to read.
Hero Vired is a leading LearnTech company dedicated to offering cutting-edge programs in collaboration with top-tier global institutions. As part of the esteemed Hero Group, we are committed to revolutionizing the skill development landscape in India. Our programs, delivered by industry experts, are designed to empower professionals and students with the skills they need to thrive in today’s competitive job market.
