Sorting is one of the major tasks in programming or development as it demonstrates the common use case in various fields such as databases, searching, rankings, etc. There are various sorting algorithms with different time and space complexities. Among these algorithms, Merge Sort stands out for its dependability and efficiency. In this article, we will see what is a Merge Sort, its algorithm, and pseudocode, demonstrate how it is implemented in the C programming language, and offer a concrete example to gain more practical experience.
Merge Sort is like a quick sort that uses the divide and conquer approach to sort the elements. It comes under the efficient algorithm against all of the sorting algorithms.
What is Sorting?
Sorting is a process in which the elements are placed at their correct position in order. The order of sorting can be ascending or descending. In other words, Sorting is the process of putting information in a particular order, usually either descending or ascending. It consists of data of complicated objects, strings, or numbers. Efficient ways for doing this rearrangement are sorting algorithms.
For example, say we have an array of elements [4, 2, 7, 11, 9, 1, 8] and now we want to sort it in ascending order, then the order after applying sorting will be [1, 2, 4, 7, 8, 9, 11].

POSTGRADUATE PROGRAM IN
Multi Cloud Architecture & DevOps
Master cloud architecture, DevOps practices, and automation to build scalable, resilient systems.
What is Merge Sort?
Merge Sort is a sorting algorithm in programming that follows the divide-and-conquer approach. It was created by J.V. Neumann in 1945. It was made for its effectiveness with big datasets because it provides the O(n log n) time complexity. The divide-and-conquer tactic is employed by the comparison-based sorting algorithm known as merge sort. In other words, it is a way in which the array is split into two halves (sub-arrays), sorting is done in each half, and then merging the two sorted halves (sub-arrays) again together.
By using recursion, the above process of merge sort continues till the array elements are sorted. Now, let’s see the working of the merge sort in C.
How does Merge Sort work?
Merge sort is the efficient and stable sorting algorithm in C to sort the elements of an array. It uses the divide and conquer method to sort the array elements. Merge Sort operates in the following steps:
- Divide:
The array is recursively divided into two sub-arrays until each half is left only with a single element. - Conquer:
Next, each sub-array is sorted individually. Here, the base case of the recursion is reached when each sub-array has one element, meaning it is already sorted. - Combine:
The sorted sub-arrays or halves are then merged back together to form a larger sorted array.
Let’s see the working of the merge sort algorithm in detail and with an example:
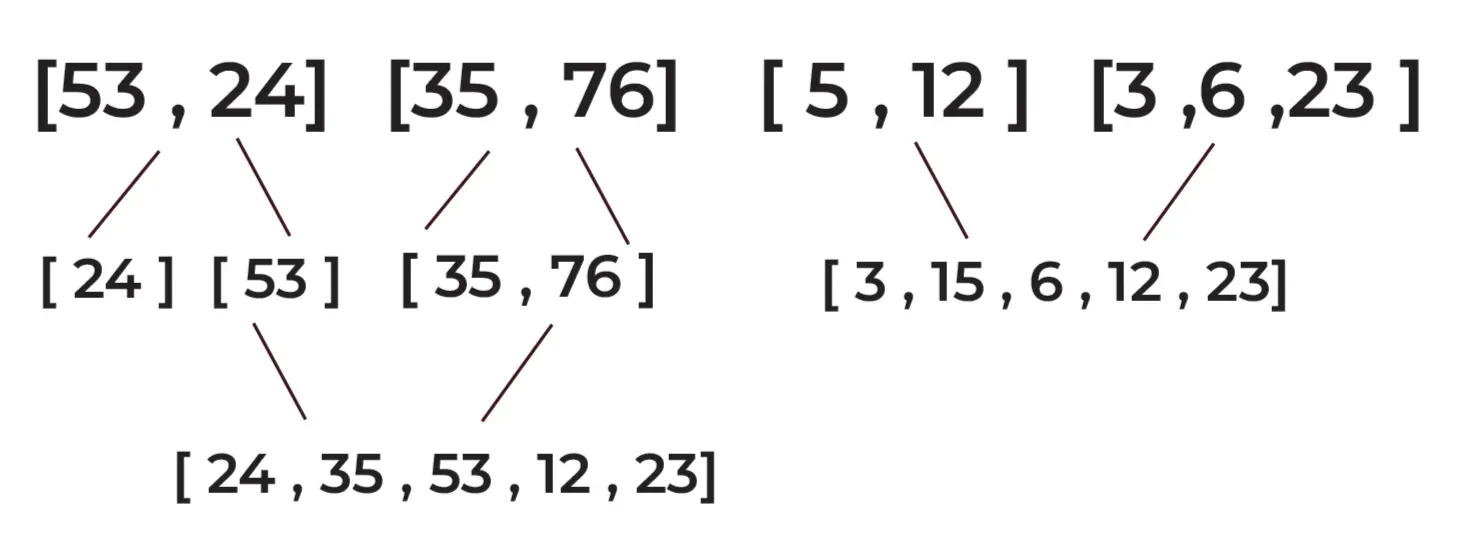
Consider an array of elements: [53, 24, 35, 76, 12, 5, 3, 6, 23]
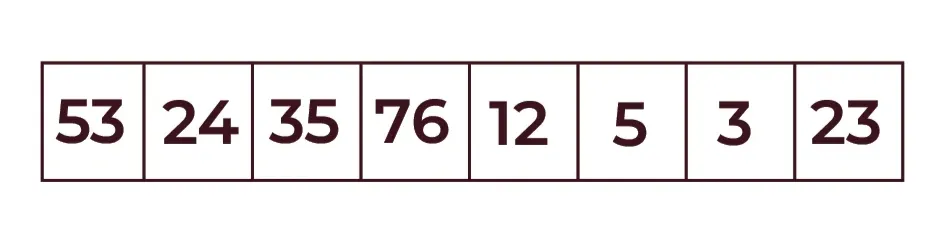
Step 1: Divide the array into sub-arrays (two halves):
firstHalf: [53, 24, 35, 76], secondHalf: [12, 5, 3, 6, 23]
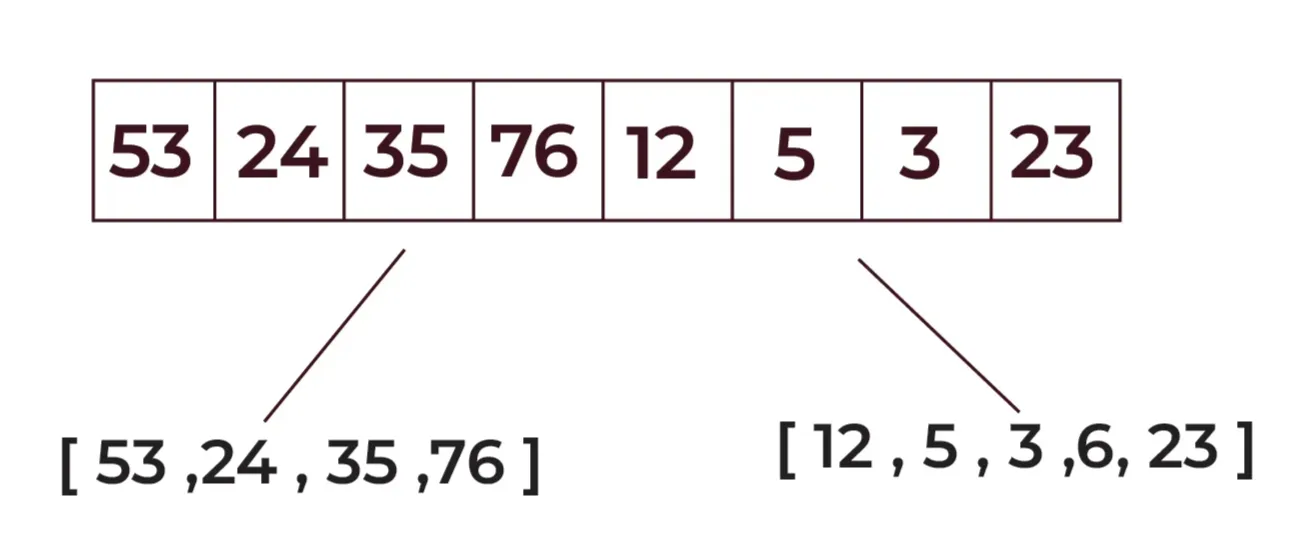
Step 2: Now recursively divide the sub-arrays:
firstHalf: [53, 24, 35, 76] becomes [53, 24] and [35, 76]
secondHalf: [12, 5, 3, 6, 23] becomes [12, 5] and [3, 6, 23]
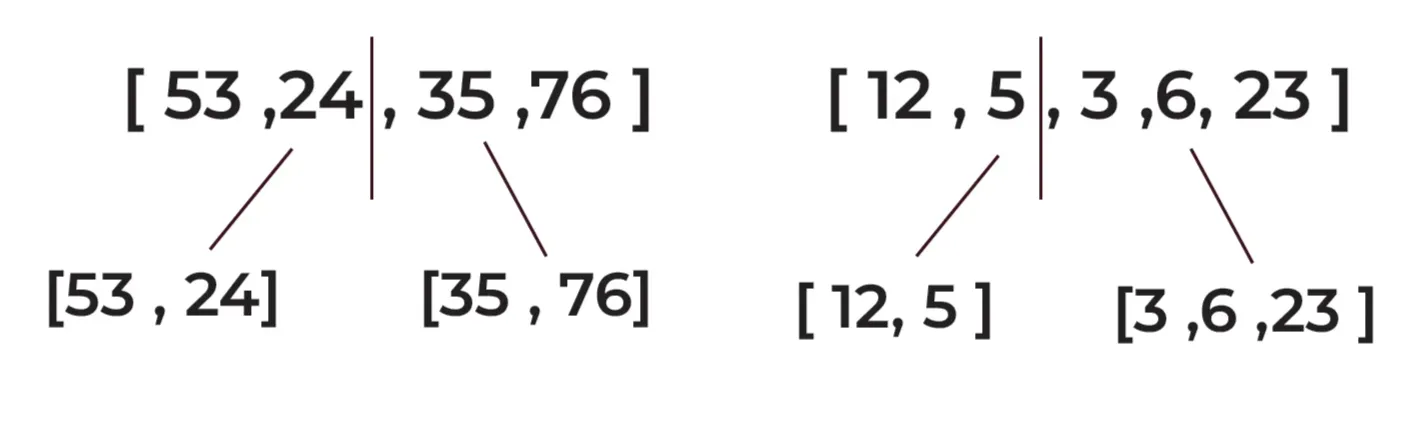
Step 3: Continue dividing (splitting) the arrays until each sub-array is left only with a single element:
[53, 24] becomes [53] and [24]
[35, 76] becomes [35] and [76]
[12, 5] becomes [12] and [5]
[3, 6, 23] becomes [3] and [6, 23]
[6, 23] becomes [6] and [23]
Now, each array element is split till all of them are left individually in the array. It is now ready to merge into one array again after doing sorting.
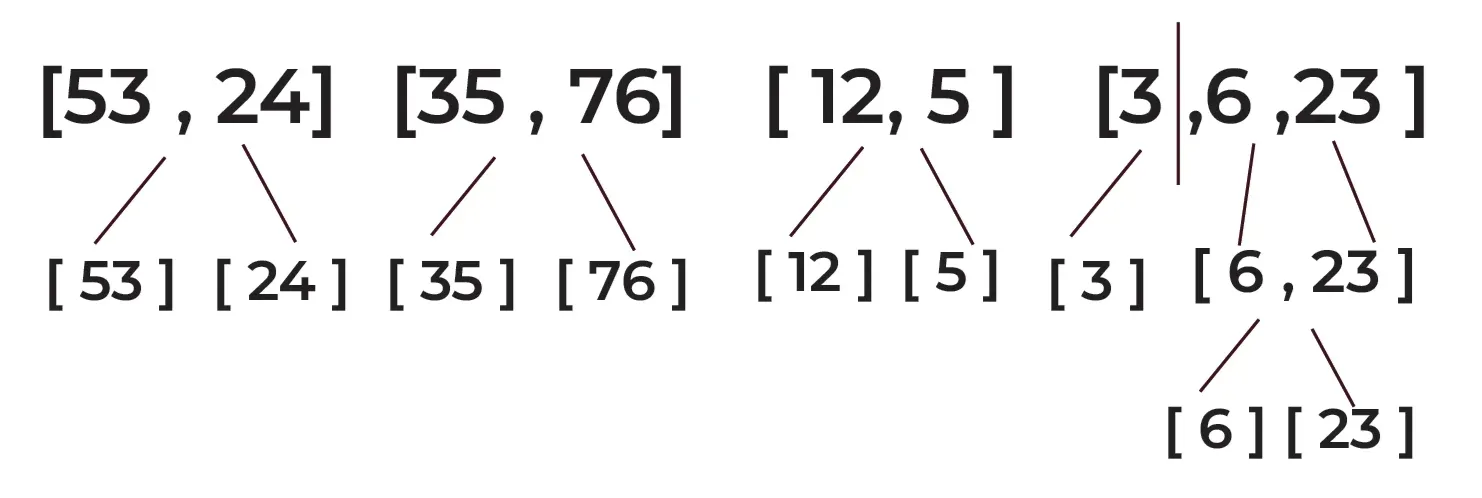
Step 4: Merge the sorted sub-arrays:
Merge [53] and [24] to get [24, 53]
Merge [35] and [76] to get [35, 76]
Merge [12] and [5] to get [5, 12]
Merge [6] and [23] to get [6, 23]
Step 5: Merge the final two sub-arrays to get the sorted array:
Merge [24, 53] and [35, 76]
Compare 24 and 35: Take 24
Compare 53 and 35: Take 35
Compare 53 and 76: Take 53
Remaining elements: 76, Output: [24, 35, 53, 76]
Merge [5, 12] and [3, 6, 23]
Compare 5 and 3: Take 3
Compare 5 and 6: Take 5
Compare 12 and 6: Take 6
Compare 12 and 23: Take 12
Remaining elements: 23, Output: [3, 5, 6, 12, 23]
Merge [24, 35, 53, 76] and [3, 5, 6, 12, 23]
Compare 24 and 3: Take 3
Compare 24 and 5: Take 5
Compare 24 and 6: Take 6
Compare 24 and 12: Take 12
Compare 24 and 23: Take 23
Remaining elements: 24, 35, 53, 76
The final array after sorting will be: [3, 5, 6, 12, 23, 24, 35, 53, 76]
That’s how the merge sort algorithm works. Let’s see the code example for implementing the merge sort algorithm in the C program.
Algorithm for Merge Sort
Pseudocode
Let’s see the pseudocode for the implementation of merge sort using a recursive approach.
mergeSort(arr[], left, right)
If left < right
- Find the middle point to divide the array into two halves:
mid = (left + right) / 2
- Call MergeSort for the first half:
mergeSort(arr, left, mid)
- Call MergeSort for the second half:
mergeSort(arr, mid + 1, right)
- Merge the two halves sorted above:
mergeTwoHalves(arr, left, mid, right)
mergeTwoHalves(arr[], left, mid, right)
n1 = mid – left + 1
n2 = right – mid
Create temp arrays t1[n1] and t2[n2]
Copy data to temp arrays t1[] and t2[]
Merge the temp arrays back into arr[left..right]
Copy the remaining elements of t1[], if any
Copy the remaining elements of t2[], if any
Explanation:
In this pseudocode, we have defined two functions. The mergeSort() function is responsible for dividing the array elements into sub-arrays or halves for sorting, whereas the mergeTwoHalves() is responsible for merging the two split arrays in temporary arrays and converting them again to the original array.
The mergeTwoHalves() is a significant function as it performs the merging of two sorted sub-arrays, to build a single sorted array.
Example:
#include <stdio.h>
#include <stdlib.h>
// Function to merge two subarrays
void mergeTwoHalves(int arr[], int left, int mid, int right) {
int i, j, k;
int n1 = mid - left + 1;
int n2 = right - mid;
// Create two temporary arrays
int temp1[n1], temp2[n2];
// Copy data to temporary arrays
for (i = 0; i < n1; i++)
temp1[i] = arr[left + i];
for (j = 0; j < n2; j++)
temp2[j] = arr[mid + 1 + j];
// Merge the temporary arrays back into arr[left..right]
i = 0; // Initial index of first subarray
j = 0; // Initial index of second subarray
k = left; // Initial index of merged subarray
while (i < n1 && j < n2) {
if (temp1[i] <= temp2[j]) {
arr[k] = temp1[i];
i++;
} else {
arr[k] = temp2[j];
j++;
}
k++;
}
// Copy the remaining elements of temp1[], if any
while (i < n1) {
arr[k] = temp1[i];
i++;
k++;
}
// Copy the remaining elements of temp2[], if any
while (j < n2) { arr[k] = temp2[j]; j++; k++; } } // Function to perform Merge Sort void mergeSort(int arr[], int left, int right) { if (right > left) {
// Get the midpoint to divide into two halves
int mid = (left + right) / 2;
// Sort first and second sub arrays
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// Merge the sorted halves
mergeTwoHalves(arr, left, mid, right);
}
}
// Function to print an array
void showArray(int num[], int s) {
for (int i = 0; i < s; i++)
printf("%d ", num[i]);
printf("\n");
}
// Main function
int main() {
int sizeOfArr;
printf("Enter the size of the array: ");
scanf("%d", &sizeOfArr);
int arr[sizeOfArr];
printf("Enter %d elements in the array to apply merge sort:\n", sizeOfArr);
for (int i = 0; i < sizeOfArr; i++) {
scanf("%d", &arr[i]);
}
int sizeOfArray = sizeof(arr) / sizeof(arr[0]);
printf("Original array before sorting is: \n");
showArray(arr, sizeOfArray);
mergeSort(arr, 0, sizeOfArray - 1);
printf("\nSorted array is: \n");
showArray(arr, sizeOfArray);
return 0;
}
Output:
// For input of odd size of array elements.
Enter the size of the array: 9
Enter 9 elements in the array to apply merge sort:
53 24 35 76 12 5 3 6 23
Original array before sorting is:
53 24 35 76 12 5 3 6 23
Sorted array is:
3 5 6 12 23 24 35 53 76
// For input of even size of array elements.
Enter the size of the array: 12
Enter 12 elements in the array to apply merge sort:
6 7 3 89 23 44 66 23 54 77 87 10
Original array before sorting is:
6 7 3 89 23 44 66 23 54 77 87 10
Sorted array is:
3 6 7 10 23 23 44 54 66 77 87 89
Explanation:
In this example, we are given an array of elements that need to be sorted using the merge sort algorithm. The division of an array (arr) into halves continues recursively using the mergeSort() function until every sub-array has only one element.
This sorted sub-arrays recombination is what the function mergeTwoHalves takes care of by comparing elements from both sub-arrays and placing them in order back into the original array. The output of the array (both before and after sorting) is handled in the main function by showArray() function.
Time Complexity:
O(n log n)
The time complexity is O(n log n) because we are splitting the array in half at each division step, the array is split into two halves, which takes O(log n) time for n elements in the array and since there are O(log n) layers of recursion and merging happens at each level, the total time required for the merging process to occur across all levels is O(n log n).
Space Complexity:
O(N)
Because Merge Sort needs to keep the temporary arrays used during the merge operation, it needs extra space proportional to the size of the array being sorted. Therefore, the space complexity is O(n) due to this extra space.

82.9%
of professionals don't believe their degree can help them get ahead at work.
Advantages and Disadvantages of Merge Sort
Below are some of the advantages and disadvantages of Merge Sort in C:
Advantages
- With a guaranteed time complexity of O(n log n), merge sort is effective when working with big datasets.
- Merge sort is a stable sorting algorithm as it maintains the order of equal elements in the array.
- Merge Sort is best when there is a usage of multi-threading and parallel processing due to its divide-and-conquer strategy.
- When sorting data that is too big to fit in memory, Merge Sort works great for external sorting. It is able to sort data that is stored on external storage devices, by combining the sections of sorted data of an array.
Disadvantages
- The very first disadvantage of merge sort is it requires additional memory space to the size of the array. It results in a space complexity of O(n), where n is the size of the temporary array.
- The traversal in merge sort is whole even if the array elements are sorted.
- Merge sort is slower as compared to other sorting algorithms.
- In comparison to simpler algorithms like Insertion Sort, the technique is less efficient for smaller datasets due to its recursive nature and potential cost caused by the use of temporary arrays. This results in an overhead issue.
Comparison with other sorting algorithms
Merge sort, being a greatly optimised sorting algorithm, can be compared with different other sorting algorithms on the basis of performance, time complexity, space complexity, stability, etc. Let’s see some of the important and useful comparisons of the merge sort algorithm with other sorting algorithms:
| Criteria | Merge Sort | Quick Sort | Insertion Sort | Heap Sort |
| Divide and Conquer | Merge sort uses the divide and conquer approach. | Quick Sort uses the divide and conquer approach. | Insertion sort does not use the divide and conquer approach. | Heap sort does not use the divide and conquer approach. |
| Time Complexity (Best) | O(n log n) | O(n log n) | O(n) | O(n log n) |
| Time Complexity (Worst) | O(n log n) | O(n^2) | O(n^2) | O(n log n) |
| Time Complexity (Average) | O(n log n) | O(n log n) | O(n^2) | O(n log n) |
| Space Complexity | O(n) | O(log n) | O(1) | O(1) |
| Stability | It is a stable sorting algorithm. | It is not a stable sorting algorithm. | It is a stable sorting algorithm. | It is not a stable sorting algorithm. |
| Recursive | A recursive approach can be used in merge sort. | The recursive approach can be used in quick sort. | A recursive approach can be used in insertion sort. | The recursive approach can’t be used in heap sort. |
| Adaptive | It is not adaptive. | It is not adaptive. | It is adaptive only for nearly sorted elements of the array. | It is not adaptive. |
| Parallelizable | Yes | Yes | No | Yes |
| Applications | Merge sort applications are in large datasets, external sorting, etc. | Quick sort applications are in internal sorting. | Insertion sort applications are in smaller datasets and those with nearly sorted data. | Heap sort applications are in priority queues and heaps. |
Conclusion
This article has given a detailed explanation of merge sort in C. We also demonstrated through an example how an array can be sorted using Merge Sort. We compared Merge Sort with Quick Sort, Heap Sort, and Insertion Sort to show the strengths and weaknesses of each sorting algorithm.
Merge Sort is an algorithm that any programmer dealing with large data sets or looking for reliable sorting methods must have heard of. Merge sort provides the best time and space complexity in the C program to sort the elements of the array. To be able to increase the efficiency and reliability of your data processing operations, you should be familiar with this algorithm.
What is the Merge sort in C?
What is the Time Complexity of Merge Sort in C?
Why should I use Merge Sort over other sorting algorithms?
Can I use Merge Sort for sorting linked lists??
Which is faster merge or insertion sort?
Updated on September 5, 2024
