The Floyd-Warshall algorithm belongs to the important areas in the field of computer science which finds the shortest distance between all pairs of vertices in a weighted digraph. It handles graphs with edge weights having positive and negative values. This time-efficient method is necessary to solve many problems of networks and graphs in which the computation of the shortest path is important.
This post will focus on explaining the Floyd-Warshall algorithm. We will explain what it does, how to implement it and write code, show complexity analysis and show real-time application.
What is a Floyd Warshall Algorithm?
The Floyd-warsahll algorithm is a method for finding the shortest path between each pair of points (nodes) within a graph. It is a relational representation where points or nodes are connected to each other by edges containing a given value such as travel distance or travel time. The objectives are to minimise the total travel duration while covering all the lines connected by edges.
Here’s how it works in simple steps:
First of all, it considers the distance between two nodes in the graph if there is any direct edge between them.
Then, it compares the length of a hypothetical path through another point and if it is shorter. To illustrate if you travel A to C, the algorithm considers B within the trip to check how far it may go.
It does this for all undirected edges and virtually every possible unordered pair of vertices on the graph.
In the end, it prepares the table demonstrating the minimum distance across all the vertices.
This way, you can definitely determine the shortest path that traverses all the points.
Get curriculum highlights, career paths, industry insights and accelerate your technology journey.
Download brochure
Step-by-Step Floyd Warshall Algorithm
Initialise the Distance Matrix:
Create a 2D matrix to store the distance between every 2 nodes in the given graph.
Initially, if there is an edge between two nodes, the distance is the weight of that edge. If there is no edge, set the distance to infinity (INF). The diagonal elements (distance from a node to itself) are set to zero.
2. Choose an Intermediate Node:
The algorithm works by iterating over each node as an “intermediate” node. For each intermediate node k, it checks if a path from node i to node j can be shortened by going through k.
3. Update Shortest Paths:
In this step, we can state that the distance between every two nodes is calculated after looking at every remaining node as a middle node. If the distance between node ‘i’ and ‘j’ is greater than the distance node ‘i’ –> node ‘k’ –> node ‘j’, update the distance between nodes for node ‘i’ and node ‘j’ in the distance matrix.
4. Repeat for All Nodes:
Repeat the above process for all nodes k, considering each one as an intermediate node, and updating the distances accordingly.
5. Final Distance Matrix:
After all nodes have been considered as intermediates, the matrix will hold the shortest distances between every pair of nodes.
Algorithm Walkthrough
Here, we have provided a detailed walkthrough to find the distance between each node shown in the below diagram.
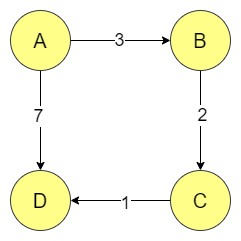
The initial distance matrix for the graph looks like this:
A B C D
A 0 3 ∞ 7
B ∞ 0 2 ∞
C ∞ ∞ 0 1
D ∞ ∞ ∞ 0
Step 1: Initialise the Distance Matrix
We start by initialising the distance matrix as a copy of the graph matrix. Initially, it looks like this:
A B C D
A 0 3 ∞ 7
B ∞ 0 2 ∞
C ∞ ∞ 0 1
D ∞ ∞ ∞ 0
Step 2: Use A as an Intermediate Node
We now try to use node A as an intermediate node and check if it can shorten any of the current paths.
For pair (B, C): No update because dist[B][A] + dist[A][C] = ∞ + ∞ = ∞.
For pair (B, D): No update because dist[B][A] + dist[A][D] = ∞ + 7 = ∞.
For pair (C, D): No update because dist[C][A] + dist[A][D] = ∞ + 7 = ∞.
No changes are made to the matrix in this step, so it remains the same:
A B C D
A 0 3 ∞ 7
B ∞ 0 2 ∞
C ∞ ∞ 0 1
D ∞ ∞ ∞ 0
Step 3: Use B as an Intermediate Node
Next, we use node B as an intermediate node and check for possible shorter paths:
For pair (A, C): dist[A][B] + dist[B][C] = 3 + 2 = 5 (which is smaller than ∞), so we update dist[A][C] to 5.
For pair (A, D): No update because dist[A][B] + dist[B][D] = 3 + ∞ = ∞.
For pair (C, D): No update.
The matrix after this step is updated as:
A B C D
A 0 3 5 7
B ∞ 0 2 ∞
C ∞ ∞ 0 1
D ∞ ∞ ∞ 0
Step 4: Use C as an Intermediate Node
Now, we use node C as an intermediate node and check for shorter paths:
For pair (A, B): No update because dist[A][C] + dist[C][B] = 5 + ∞ = ∞ (which is greater than 3).
For pair (A, D): dist[A][C] + dist[C][D] = 5 + 1 = 6 (which is smaller than 7), so we update dist[A][D] to 6.
For pair (B, D): dist[B][C] + dist[C][D] = 2 + 1 = 3, so we update dist[B][D] to 3.
The matrix after this step is updated to:
A B C D
A 0 3 5 6
B ∞ 0 2 3
C ∞ ∞ 0 1
D ∞ ∞ ∞ 0
Step 5: Use D as an Intermediate Node
Finally, we use node D as an intermediate node and check for possible shorter paths. However, since all paths involving node D are already optimal, no further updates are made to the matrix in this step.
Final Distance Matrix
A B C D
A 0 3 5 6
B ∞ 0 2 3
C ∞ ∞ 0 1
D ∞ ∞ ∞ 0
Code Examples
Java
public class FloydWarshall {
// Define a large value to represent "infinity" (no direct path)
final static int INF = 99999;
public void floydWarshall(int graph[][]) {
int numVertices = graph.length;
// Create a 2D array to store shortest distances between every pair of nodes
int distance[][] = new int[numVertices][numVertices];
// Initialize the solution matrix by copying the input graph matrix
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
distance[i][j] = graph[i][j];
}
}
// Update the distance matrix by considering each vertex as an intermediate point
for (int node = 0; node < numVertices; node++) {
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
// If the path through vertex 'node' is shorter, update the distance
if (distance[i][node] + distance[node][j] < distance[i][j]) {
distance[i][j] = distance[i][node] + distance[node][j];
}
}
}
}
// Print the final shortest distance matrix
printSolution(distance);
}
// Method to print the matrix with shortest distances
void printSolution(int distance[][]) {
int numVertices = distance.length;
System.out.println("Shortest distances between every pair of vertices:");
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
if (distance[i][j] == INF) {
System.out.print("INF ");
} else {
System.out.print(distance[i][j] + " ");
}
}
System.out.println();
}
}
public static void main(String[] args) {
// Define a graph with 4 nodes (represented by a 2D array)
int graph[][] = {
{0, 3, INF, 7},
{INF, 0, 2, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
// Create an object of the class and call the floydWarshall method
FloydWarshall algorithm = new FloydWarshall();
algorithm.floydWarshall(graph);
}
}
Python
INF = 99999
# Method to implement Floyd-Warshall algorithm
def floydWarshall(graph):
numVertices = len(graph)
dist = [[graph[i][j] for j in range(numVertices)] for i in range(numVertices)]
# Update the distance matrix by considering each vertex as an intermediate point
for k in range(numVertices):
for i in range(numVertices):
for j in range(numVertices):
# If the path through vertex 'k' is shorter, update the distance
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
# Print the final shortest distance matrix
printSolution(dist)
# Method to print the matrix with shortest distances
def printSolution(dist):
numVertices = len(dist)
print("Shortest distances between every pair of vertices:")
for i in range(numVertices):
for j in range(numVertices):
if dist[i][j] == INF:
print("INF", end=" ")
else:
print(dist[i][j], end=" ")
print()
if __name__ == "__main__":
graph = [
[0, 3, INF, 7],
[INF, 0, 2, INF],
[INF, INF, 0, 1],
[INF, INF, INF, 0]
]
# Call the floydWarshall method
floydWarshall(graph)
C
#include <stdio.h>
#define INF 99999
#define NUM_VERTICES 4
void printSolution(int dist[NUM_VERTICES][NUM_VERTICES]) {
int i, j;
printf("Shortest distances between every pair of vertices:n");
for (i = 0; i < NUM_VERTICES; i++) {
for (j = 0; j < NUM_VERTICES; j++) {
if (dist[i][j] == INF) {
printf("INF ");
} else {
printf("%d ", dist[i][j]);
}
}
printf("n");
}
}
// Method to implement Floyd-Warshall algorithm
void floydWarshall(int graph[NUM_VERTICES][NUM_VERTICES]) {
int dist[NUM_VERTICES][NUM_VERTICES], i, j, k;
// Initialize the solution matrix by copying the input graph matrix
for (i = 0; i < NUM_VERTICES; i++) {
for (j = 0; j < NUM_VERTICES; j++) {
dist[i][j] = graph[i][j];
}
}
// Update the distance matrix by considering each vertex as an intermediate point
for (k = 0; k < NUM_VERTICES; k++) {
for (i = 0; i < NUM_VERTICES; i++) {
for (j = 0; j < NUM_VERTICES; j++) {
// If the path through vertex 'k' is shorter, update the distance
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// Print the final shortest distance matrix
printSolution(dist);
}
int main() {
int graph[NUM_VERTICES][NUM_VERTICES] = {
{0, 3, INF, 7},
{INF, 0, 2, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
// Call the floydWarshall method
floydWarshall(graph);
return 0;
}
C++
#include <iostream>
using namespace std;
#define INF 99999
#define NUM_VERTICES 4
// Method to print the matrix with shortest distances
void printSolution(int dist[NUM_VERTICES][NUM_VERTICES]) {
cout << "Shortest distances between every pair of vertices:n";
for (int i = 0; i < NUM_VERTICES; i++) {
for (int j = 0; j < NUM_VERTICES; j++) {
if (dist[i][j] == INF) {
cout << "INF ";
} else {
cout << dist[i][j] << " ";
}
}
cout << endl;
}
}
void floydWarshall(int graph[NUM_VERTICES][NUM_VERTICES]) {
int dist[NUM_VERTICES][NUM_VERTICES];
// Initialize the solution matrix by copying the input graph matrix
for (int i = 0; i < NUM_VERTICES; i++) {
for (int j = 0; j < NUM_VERTICES; j++) {
dist[i][j] = graph[i][j];
}
}
// Update the distance matrix by considering each vertex as an intermediate point
for (int k = 0; k < NUM_VERTICES; k++) {
for (int i = 0; i < NUM_VERTICES; i++) {
for (int j = 0; j < NUM_VERTICES; j++) {
// If the path through vertex 'k' is shorter, update the distance
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// Print the final shortest distance matrix
printSolution(dist);
}
int main() {
int graph[NUM_VERTICES][NUM_VERTICES] = {
{0, 3, INF, 7},
{INF, 0, 2, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
// Call the floydWarshall method
floydWarshall(graph);
return 0;
}
JavaScript
const INF = 99999;
// Method to implement Floyd-Warshall algorithm
function floydWarshall(graph) {
let numVertices = graph.length;
// Create a 2D array to store shortest distances between every pair of nodes
let dist = Array.from({ length: numVertices }, (_, i) =>
graph[i].slice()
);
// Update the distance matrix by considering each vertex as an intermediate point
for (let k = 0; k < numVertices; k++) {
for (let i = 0; i < numVertices; i++) {
for (let j = 0; j < numVertices; j++) {
// If the path through vertex 'k' is shorter, update the distance
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// Print the final shortest distance matrix
printSolution(dist);
}
// Method to print the matrix with shortest distances
function printSolution(dist) {
let numVertices = dist.length;
console.log("Shortest distances between every pair of vertices:");
for (let i = 0; i < numVertices; i++) {
let row = "";
for (let j = 0; j < numVertices; j++) {
if (dist[i][j] === INF) {
row += "INF ";
} else {
row += dist[i][j] + " ";
}
}
console.log(row);
}
}
let graph = [
[0, 3, INF, 7],
[INF, 0, 2, INF],
[INF, INF, 0, 1],
[INF, INF, INF, 0]
];
// Call the floydWarshall method
floydWarshall(graph);
Output
Shortest distances between every pair of vertices:
0 3 5 6
INF 0 2 3
INF INF 0 1
INF INF INF 0
Complexity Analysis
Time Complexity
The Floyd-Warshall algorithm uses three nested loops to calculate the shortest paths between all pairs of nodes in the graph. These loops iterate over the vertices of the graph:
The outer loop runs n times (where n is the number of vertices in the graph), checking each vertex as an intermediate node.
For each iteration of the outer loop, there are two inner loops that each run n times to examine all pairs of start and end nodes.
So, the total number of operations performed by the algorithm is proportional to n3. Therefore, the time complexity is: O(n³)
This makes the Floyd-Warshall algorithm less efficient for very large graphs, but it is suitable for smaller graphs or dense graphs where all pairs of shortest paths are required.
The algorithm requires a 2D matrix to store the shortest distances between all pairs of nodes. This matrix has n × n elements, where n is the number of nodes. Since the space used is directly proportional to the number of nodes, the space complexity is: O(n²)
Additionally, in the code provided, the dist matrix is a separate copy of the original graph matrix, so it requires O(n²) additional space.
Real-World Applications of the Floyd-Warshall Algorithm
Here are some important fields where it is used:
Routing in Communication Networks: In such cases, the algorithm sequentially finds the paths of minimum length from the source node to each of the constituent nodes.
Graph Analysis: It can be used in solving problems related to reachability and connectivity in directed graphs.
Social Network Analysis: It is useful for determining the length of the shortest path between individuals or entities within a social network.
Game Theory: In certain strategy games, it helps to calculate optimal moves by finding the shortest paths on game boards or maps
Transportation Networks: It helps in finding the shortest route between cities or locations in logistics and transportation systems.
Alternatives of the Floyd-Warshall Algorithm
Dijkstra’s Algorithm
Dijkstra’s aim is to calculate the optimal path from one node to any other node in the graph with no negative weights. It follows graph theory whereby a vertex called the source is chosen and then the least known distance is consistently chosen which is then used to update the distances of the adjacent vertices until all of them have been processed. This process continues until all the nodes have been processed.
Key points about this algorithm Dijkstra:
Single-source shortest path: Finds the shortest path from a single node to all other nodes.
Non-negative edge weights: Works only with graphs where all edge weights are non-negative.
Simple greedy strategy: At each step, it selects a vertex which has the minimum distance from the already computed distances.
Time complexity: O(V2) using an adjacency matrix or O((V + E) log V) with priority queue where V is vertices count and E is edges count.
Space complexity: O(V) for storing the shortest distance from the source to any node.
Bellman-Ford Algorithm
The Bellman-Ford algorithm is used for finding the shortest path in the condition of one source node to all remaining nodes of the graph, as Dijkstra’s approach. Dijkstra’s algorithm is used for graphs that do not have negative edges.
Key points about the Bellman-Ford algorithm:
Single-source shortest path: Determines the shortest path coming out of a single node to all the other nodes.
Handles negative weights: Bellman-Ford sets itself apart from Dijkstra’s algorithm in that it can be used on graphs that bear edges with negative weights.
Edge relaxation: The number of edges of the graph is relaxed V-1 times, them being the number of vertices V in the graph.
Time complexity: O(V × E), where V and E are the total number of vertices and number of edges respectively.
Detects negative cycles: This feature finds the presence of negative cycles and therefore serves its purpose in some of the problems which are concerned with this.
Difference between the Floyd-Warshall Algorithm and Dijkstra’s Algorithm
Feature
Floyd-Warshall Algorithm
Dijkstra’s Algorithm
Purpose
Finds the shortest paths between all pairs of nodes
Finds the shortest path from a single source to all other nodes
Graph Type
Works with graphs that have positive or negative edge weights (no negative cycles)
Works with graphs that have only non-negative edge weights
Time Complexity
O(V³), where V is the number of vertices
O(V²) with adjacency matrix, O((V + E) log V) with priority queue (V: vertices, E: edges)
Space Complexity
O(V²)
O(V), as it stores distance values for each vertex
Approach
Dynamic programming
Greedy approach
Cycle Handling
Can handle negative edge weights but not negative cycles
Does not handle negative edge weights
When to Use
When the shortest path between all pairs of nodes is required
When the shortest path from a single source is required and the graph has non-negative weights
Difference between the Floyd-Warshall Algorithm and the Bellman-Ford Algorithm
Feature
Floyd-Warshall Algorithm
Bellman-Ford Algorithm
Purpose
Finds the shortest paths between all pairs of nodes
Finds the shortest path from a single source to all other nodes
Graph Type
Works with graphs that have positive or negative edge weights (no negative cycles)
Works with graphs that may have negative edge weights, including negative cycles
Time Complexity
O(V³), where V is the number of vertices
O(V × E), where V is the number of vertices and E is the number of edges
Space Complexity
O(V²)
O(V), as it stores distance values for each vertex
Approach
Dynamic programming
Iterative edge relaxation
Cycle Handling
Can handle negative edge weights but not negative cycles
Can detect negative weight cycles in the graph
When to Use
When the shortest path between all pairs of nodes is required
When negative edge weights are present or when cycle detection is needed
The Floyd-Warshall algorithm is efficient in determining the shortest distances between any two nodes in a weighted directed graph. This is very important in a number of applications including routing and conducting network analysis as it can cope with graphs where edges have both positive and negative weights. Its cubic time complexity means that it is not the best algorithm to apply on very large graphs.
In contrast, there are algorithms that are relatively faster in solving the single source shortest path such as Dijkstra’s algorithm as well as negative weight shortest paths such as the Bellman-Ford algorithm, Floyd-Warshall remains the ultimate for the all-pairs shortest path problem.
FAQs
What’s the purpose of the Floyd-Warshall algorithm?
This helps in finding the shortest paths of all the pairs of the nodes in the graph.
Can Floyd-Warshall work with negative weights for edges?
Yes, but it cannot work if there are negative weight cycles within the graph.
What is the order of computational complexity of the Floyd-Warshall algorithm?
The time complexity is Time O(V³), where V is the vertices in the algorithm applied.
How much space does the Floyd-Warshall take?
The space complexity is O(V²) since it uses a 2D distance matrix.
Is it possible for Bellman-Ford to identify negative circles?
Yes, Bellman-Ford can identify existing circles which possess negative weights on the vertices of the graph.
Hero Vired is a leading LearnTech company dedicated to offering cutting-edge programs in collaboration with top-tier global institutions. As part of the esteemed Hero Group, we are committed to revolutionizing the skill development landscape in India. Our programs, delivered by industry experts, are designed to empower professionals and students with the skills they need to thrive in today’s competitive job market.
