Abstract Data Type in Data Structure – Explained with Examples

Before understanding ADT, let us consider the different built-in data types that were given to us. In-built data types are int, float, double, long, etc. We can do basic operations like addition, subtraction, division, multiplication, etc. But we may be at a time when we need to define operations for our user-defined data type. They can only be defined as and when we need them. The problem-solving process can be reduced by creating an actual data structure along with its operations like Abstract Data Type (ADT) because such data structure, which is not in-built, is called Abstract Data type.

Understanding Abstract Data Type

An ADT is analogous to an algebraic structure in mathematics, consisting of a domain, a collection of operations, and a set of constraints these operations must satisfy. The domain is often implicitly defined as the free object over the set of ADT operations. The interface of the ADT refers to the domain and operations and may include constraints like preconditions and postconditions but not behavioural relations between operations. As the image shows, an ADT comprises public and private functions interacting with underlying data structures (e.g., arrays or linked lists). The application program interacts with the ADT through its interface, abstracting the complexities of the underlying data structures. Constraints, such as Last-In-First-Out for a stack or First-In-First-Out for a queue, help distinguish the behaviour of operations despite similar interfaces.

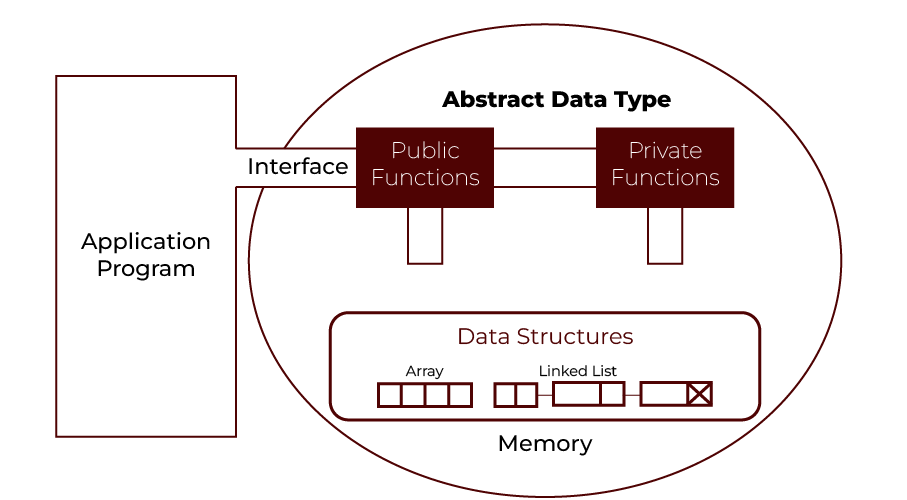
For example, in data typing, the user of that data type does not need to know how that data type is implemented, e.g. we were using Primitive values like int, float, and char type just knowing that they can be operated or performed on and yet we don’t know how they are getting their values. Thus, a user is only required to know what a data type can do, and it does not deserve a specific implementation. ADT is just a black box that conceals the data type’s structure and design.

There are two main styles for formal specifications: axiomatic semantics and operational semantics.

ADTs are formally specified in two ways:

Axiomatic Semantics:

This approach follows the principles of functional programming, where each state of an ADT is a separate value. Operations are modelled as mathematical functions with no side effects, taking the old state as an argument and returning a new state.

The constraints for these operations are expressed as axioms or algebraic laws.

Operational Semantics:

In this view, based on imperative programming, ADTs are mutable entities that can change state over time. The order of operations matters and the same operation may produce different results depending on when it is executed.

This style often describes the operations as being executed or applied, similar to imperative programming languages.

Auxiliary Operations

In addition to the primary operations, ADTs may include auxiliary operations such as:

• create(): Creates a new instance of the ADT.
• compare(s, t): Checks if two instances are equivalent.
• hash(s): Computes a hash function based on the instance’s state.
• print(s) or show(s): Provides a human-readable representation of the state.

In imperative-style definitions, other operations like initialize(s), copy(s, t), clone(t), and free(s) may also be specified. These help manage the ADT’s state and memory usage, especially when storage analysis is necessary.

Aliasing and Complexity Analysis

In ADTs, aliasing refers to scenarios where multiple instances coexist, and it may not be clear if modifying one instance affects another. To manage this, ADT definitions often assume operations apply to a single implicit instance but can be extended to handle multiple instances by explicitly including an instance parameter. For example, operations on a stack (push(S, x), pop(S)) specify which instance they apply to. A partial aliasing axiom ensures distinct instances remain independent, even for complex ADTs like trees or pointers. Complexity analysis, crucial for algorithm evaluation, specifies operation time and space costs, aiding in interchangeable module development. Complexity assertions, like those in the C++ Standard Template Library (STL), ensure modules behave functionally and perform predictably.

Examples of Different Types of ADTs

Abstract Variable

An abstract variable is the simplest form of an ADT, similar to a basic variable in programming. It supports two main operations: fetch, which retrieves the current value, and store, which updates the value. The rule is that fetch always returns the most recent value stored. For example, if you store a value in a variable and then fetch it, you’ll get it back. The store operation replaces any existing value. It’s like when you assign a value to a variable; the previous value is overwritten.

In programming, fetch is used whenever a value is needed, and store is like assigning a value (e.g., V ← x). The order of these operations matters, ensuring that changing one variable does not affect another unless explicitly intended.

Abstract Stack

An abstract stack is an ADT that follows the “Last In, First Out” (LIFO) principle. It has three main operations:

• Push: Adds a new item to the stack.
• Pop: Removes the most recent item.
• Peek (or Top): Shows the item at the top without removing it.

Stacks also include a function to check if they are empty and a method to create a new stack. For instance, if you push an item, then pop it, the stack returns to its previous state. The stack remains consistent with these operations, meaning it works predictably as items are added or removed.

Boom Hierarchy

The Boom hierarchy describes a group of related ADTs: binary trees, lists, bags, and sets. These ADTs share common operations:

• null: Creates an empty container.
• single: Creates a container with one element.
• append: Combines two containers.

Each data type builds on these operations with additional rules:

• For trees, null is neutral (it doesn’t change the container).
• Lists add that append works in sequence (order matters).
• Bags allow append to work in any order.
• Sets make append overwrite duplicates (no repeating elements).
• These rules ensure that each operation works consistently according to the ADT type.

Common ADTs

Some widely used ADTs include:

• Collections like lists, sets, and maps.

List ADT

Linear data structures that store data in a non-continuous manner. Data storage containers in the list are called “nodes.” As such, each node is linked to another node and contains the address to another block. These links thus connect all of the nodes.

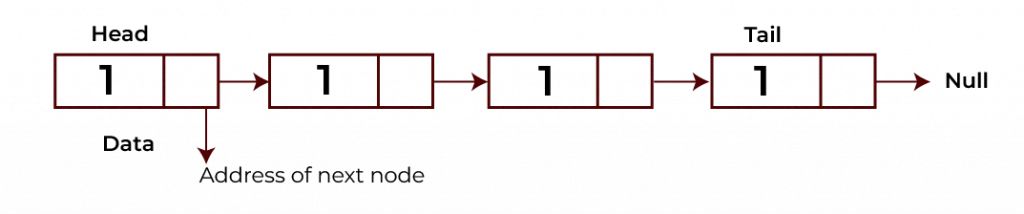
Following are some of the most important operations defined in List ADT.

• front(): It returns the value present at the front of the list.
• back(): The method returns the node’s value that lies at the back of the list.
• push_front(int val): it makes a new pointer that points to val and stores that pointer in the new head of the linked list.
• push_back(int val): This creates a pointer whose value = val and stores that pointer in the back of the linked list.
• pop_front(): It also removes the front node from the list.
• pop_back(): It removes the last node from the list.
• empty(): if the list is empty, it returns true, otherwise it returns false.
• size(): It returns the number of nodes in a list.

• Linear structures like stacks, queues, and priority queues.

Stack ADT

A linear data structure that supports insertion and deletion only from the top. It simply has two operations: push (to add data to the top of the stack) and pop (used to remove data from the top of the stack).

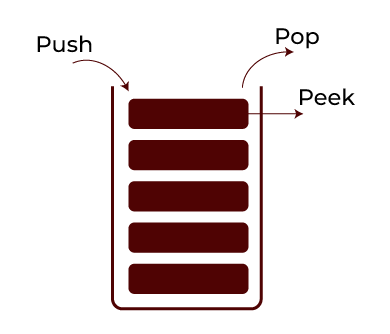
Below is the list of some of the most essential operations defined in Stack ADT.

• top(): it returns the value of the node present at the top of the stack.
• push(int val): This function puts it at the stack top and creates a node with value = val.
• pop(): It removes the node from the top of the stack.
• empty(): It returns true if the stack is empty; else, it returns false.
• size(): It returns the number of nodes in the stack.

Also Read: What is Stack in Data Structures

Queue ADT

A linear data structure is a queue accessed from two ends. There are two main operations in the queue: This operation pushes (inserting data to the back) and pop operation (removes data from the front of the queue).

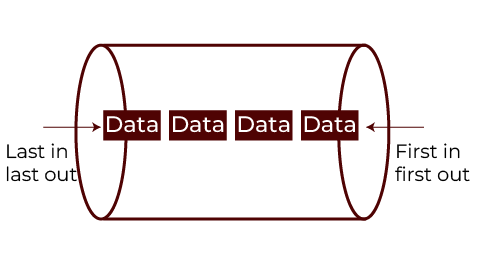
The following list is some of the most essential operations defined in Queue ADT.

• front(): It returns the node’s value in front of the node.
• back(): Value on that node at the back of the queue returns.
• push(int val): It creates a node with value = val and puts the node at the front of the queue.
• pop(): It removes the node from the rear of the queue.
• empty(): If the queue is empty, it returns true; otherwise, it returns false.
• size(): The number of nodes in the queue is returned by the returns.

Each ADT can be implemented differently, using arrays or linked lists for stacks. These choices depend on specific requirements, such as performance, but the interface remains consistent.

Also Read: Queue in Data Structure

Implementation of ADTs

ADTs are theoretical models that describe data operations and behaviour. These models are implemented using concrete data structures like arrays or linked lists. These implementations must align with the ADT’s rules, though they may have limitations, such as handling integer overflow in fixed-width numbers.

Multiple ways exist to implement the same ADT, offering flexibility based on specific needs. For instance, a stack can be implemented with arrays or linked lists. This flexibility allows code to work regardless of the specific implementation, enhancing efficiency and consistency.

Modern programming languages like Java and C++ support ADTs through classes and interfaces, allowing developers to encapsulate data structures and ensure that implementations can be changed without affecting how the ADT is used in code. Some built-in types, like arrays in scripting languages, function as ADTs by specifying their operations rather than their structure.

Abstract Graphical Data Type

An abstract graphical data type (AGDT) extends ADTs for creating structured graphical objects. It was introduced to build graphics using the advantages of ADTs, ensuring consistency and structure in graphical programming.

Conclusion

Abstract Data Types (ADTs) are a centrepiece in computer science, presenting a high-level design template for structuring and manipulating data. ADTs enable developers to encapsulate data and operations to create scalable and reusable solutions and avoid dealing with those implementation details.

Put differently, ADTs are a bridge between theory and practice, from theoretical to practical, to generate a set of versatile data structures and algorithms. By backing the ADT programming to programmers, they can shift focus from implementing the ADT and concentrate on problem solutions and efficient design, which improves the maintenance and flexibility of their codebase. ADTs still carry weight as technology changes around us, guiding the building of new features in software systems and keeping data as it is managed and manipulated. Planning to kickstart your tech career? Consider pursuing Hero Vired’s Certificate Program in Application Development offered in collaboration with Microsoft.