Binary trees are a fundamental data structure in computer science, allowing efficient organization and retrieval of data. Threaded binary trees offer unique advantages and applications among various types of binary trees. In this blog, we will explore the concept of threaded binary trees, understand their purpose, advantages, and applications, delve into traversal techniques, compare them with standard binary trees, and even discuss their implementation. So let’s dive in!
What are Threaded Binary Trees?
A threaded binary tree modifies the standard binary tree structure that provides additional information about the tree’s traversal order. In a threaded binary tree, some null pointers are replaced with references to predecessor or successor nodes. This modification enables us to navigate the tree efficiently without needing recursive algorithms or explicitly maintaining a stack.
The threading of a binary tree simplifies its traversal by creating threads, or links, that point to the in-order predecessor and successor of each node. These threads effectively eliminate the need for backtracking during traversal, improving efficiency.

POSTGRADUATE PROGRAM IN
Multi Cloud Architecture & DevOps
Master cloud architecture, DevOps practices, and automation to build scalable, resilient systems.
Purpose of Threaded Binary Trees
The primary purpose of using threaded binary trees is to optimize traversal operations, such as in-order traversal. By threading the tree, we eliminate the overhead of recursive function calls or stack-based iterations, making the traversal process more efficient. Moreover, threaded binary trees facilitate quick access to predecessor and successor nodes, which can be beneficial in various scenarios.
Advantages of Threaded Binary Trees
Below are the advantages of threaded binary trees:
- Efficient Traversal: Threaded binary trees provide efficient traversal algorithms, especially for in-order traversal. The absence of recursive function calls or explicit stack usage makes it faster and reduces the memory overhead.
- Quick Predecessor and Successor Access: Threaded binary trees allow constant time access to the in-order predecessor and successor nodes of any given node. This property is advantageous in certain applications requiring quick access to adjacent nodes.
- Space Optimization: Threading a binary tree can reduce the memory footprint compared to using additional data structures for traversal. This optimization is particularly significant when dealing with large trees or constrained memory environments.
- Simplified Code: Threaded binary trees simplify the implementation of traversal algorithms. By eliminating the need for explicit stack management or recursion, the code becomes cleaner and easier to understand.
Applications of Threaded Binary Trees
- Efficient In-order Traversal: In situations where repeated in-order traversals are required, threaded binary trees offer significant performance improvements.
- Binary Search Tree Operations: Threaded binary search trees utilize threading to enhance search, insertion, and deletion operations. The threaded structure facilitates efficient navigation and reduces the time complexity of these operations.
- Space-Constrained Environments: In memory-constrained environments, threaded binary trees can be a valuable alternative to standard binary trees. The reduced memory footprint makes them suitable for embedded systems, resource-constrained devices, or environments with limited memory.
- Database Indexing: Threaded binary trees can be used as database index structures to speed up search and retrieval operations. Their efficient traversal and quick access to predecessor and successor nodes make them ideal for maintaining sorted data.
- Threaded Binary Tree Representations: Threaded binary trees find applications in various representations, such as expression trees, syntax trees, and hierarchical data structures.

82.9%
of professionals don't believe their degree can help them get ahead at work.
Understanding Traversal Techniques in Binary Trees
Below are the traversal techniques used in threaded binary trees:
- In-order Traversal: In in-order traversal, we visit the left subtree, then the root node, and finally, the right subtree. In a threaded binary tree, in-order traversal is particularly efficient due to the threading links.
- Pre-order Traversal: Pre-order traversal visits the root node first, followed by the left subtree and then the right subtree. It is commonly used for creating a copy of the tree or evaluating arithmetic expressions.
- Post-order Traversal: Post-order traversal starts with the left subtree, then the right subtree, and finally visits the root node. It is often used for deleting or freeing the nodes of a tree.
Types of Threaded Binary Trees
Below are the 2 major types of threaded binary trees:
- Single-Threaded Binary Trees: Each node contains a link to its in-order successor or predecessor in single-threaded binary trees. However, the link to the other node (predecessor or successor) remains as a null pointer.
- Double-Threaded Binary Trees: Double-threaded binary trees, also known as fully threaded binary trees, have links to both the in-order successor and predecessor for each node. These links allow for bidirectional traversal and quick access to adjacent nodes in both directions.
Exploring the Concept of Threading in Binary Trees
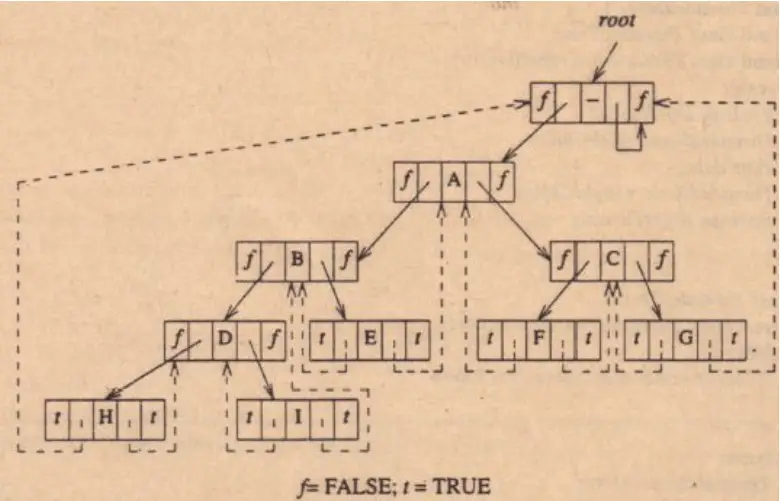
Threading in binary trees involves replacing null pointers with references to other nodes. Let’s look at the threading concept by considering an example.
Consider the following binary tree:
4
/ \
2 6
/ \ / \
1 3 5 7
To thread this tree, we replace the null pointers with threading links to each node’s in-order predecessor and successor. After threading, the tree becomes:
4
/ \
2 6
/ \ / \
1 3 5 7
/ \ / \ / \ / \
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
1 2 3 4 5 6 7 ↑ ↑
In the threaded tree, the leftmost and rightmost nodes in each subtree contain threading links that point to the in-order predecessor and successor, respectively. These links allow us to traverse the tree efficiently without additional stack usage.
Threaded Binary Trees vs. Standard Binary Trees
| Property | Standard Binary Trees | Threaded Binary Trees |
|---|---|---|
| Efficient In-order Traversal | Requires recursion or stack | Efficient without recursion or stack usage |
| Quick Predecessor and Successor Access | Requires extra operations | Constant time access |
| Space Optimization | No threading | Reduced memory footprint |
| Simplified Code | Recursive or stack-based algorithms | Simpler code without explicit stack |
Implementing Threaded Binary Trees
Implementing threaded binary trees requires careful consideration of the threading links and their maintenance during insertion, deletion, and other operations. Various algorithms and techniques can be employed to achieve efficient and correct threaded binary tree implementations.
Conclusion
Threaded binary trees provide a valuable enhancement to the standard binary tree structure by introducing threading links that optimize traversal and enable quick access to predecessor and successor nodes. They offer benefits such as efficient in-order traversal, constant time access to adjacent nodes, reduced memory footprint, and simplified code. By understanding the concept, properties, and implementation techniques of threaded binary trees, you can leverage their advantages to improve the efficiency and performance of your data structures and algorithms.
How do threaded binary trees compare to balanced binary trees?
Can threaded binary trees be used for efficient binary tree modification operations?
Are threaded binary trees suitable for dynamic data structures that require frequent insertions and deletions?
Are threaded binary trees compatible with multi-threaded or parallel programming environments?
Can threaded binary trees be used for storing and traversing non-unique values?
Updated on April 23, 2024
