Most often, decisions made on assumptions lead to costly mistakes in health care, business, and education. Hypothesis testing gives a structured approach to test such assumptions by using data to make an informed choice.
Hypothesis testing in statistics is an important technique that enables us to check assumptions and make decisions using the data about population parameters. Thus, a pharmaceutical company could require confirmation of whether a new drug was more effective than an already marketed one. They can proceed by analysing the data, therefore making conclusions with great confidence using hypothesis testing.
This method is used in nearly all fields, from appraising the effectiveness of new drugs to optimising business strategies. By examining the relationship between variables and discovering patterns, hypothesis testing in statistics takes raw data to action.
By carefully looking at and understanding data, it reduces doubt, making sure decisions are based on statistical facts. Knowing its basic ideas and uses opens up the chance to solve real-life problems correctly and confidently.
This method is not for scientists alone. Businesses use it to try out marketing strategies and teachers to check teaching methods. Hypothesis testing in statistics applies as a tool that connects data and decision-making.
Core Concepts: Null and Alternative Hypotheses Defined
Let’s take a step back before diving into the process.
Every hypothesis testing in statistics begins with two contrasting statements:
Null Hypothesis (H₀): This is the default assumption. It states that there is no effect, no difference, or no relationship. For example, “The new teaching method has no impact on student performance.”
Alternative Hypothesis (H₁): This contradicts the null hypothesis, suggesting there is an effect or difference. In the same example, it would state, “The new teaching method improves student performance.”
These are mutually exclusive hypotheses; one must be false while the other is true. Hypothesis testing in statistics seeks to identify which of the two holds under scrutiny.
Get curriculum highlights, career paths, industry insights and accelerate your management journey.
Download brochure
The Role of Significance Levels, P-Values, and Critical Values in Hypothesis Testing
When we test ideas, we need to decide when to say the null hypothesis is wrong. This choice depends on three important factors:
1. Significance Level (α)
The significance level is the threshold for making decisions. Usually set at 5% (0.05), it represents the probability of rejecting the null hypothesis when it’s actually true. Lower significance levels reduce the risk of error but require stronger evidence.
2. P-Values
The p-value reflects the strength of evidence against the null hypothesis. A small p-value (less than α) shows strong evidence to reject the null hypothesis. For example:
A p-value of 0.03 indicates that there is a 3% chance that the outcomes observed were by chance and by random variability.
3. Critical Values
Critical values differentiate the rejection region from the acceptance region on a distribution curve. If the test statistic falls in the rejection region, then the null hypothesis is rejected.
To illustrate, imagine you test a new training programme and its effect on worker performance. The null hypothesis states no improvement. You get a p-value of 0.02. Being less than the critical level of 0.05, you reject the null and conclude that the program works.
Comprehensive Steps for Conducting Hypothesis Testing
A well-structured hypothesis test follows these steps:
1. Define the Hypotheses
Start by stating the null and alternative hypotheses clearly. For instance:
H₀: “The average test score is 70.”
H₁: “The average test score is not 70.”
2. Choose the Significance Level
Decide on the acceptable risk level, often set at 0.05. This step ensures consistency and reliability in decision-making.
3. Collect and Analyse Data
Gather data from a sample that accurately represents the population. Ensure the sample size is adequate to produce meaningful results.
4. Select the Appropriate Test
The choice depends on factors like sample size and data type:
Z-Test: Large samples, known population standard deviation.
T-Test: Small samples, unknown standard deviation.
Chi-Square Test: Categorical data.
5. Calculate the Test Statistic
Use statistical formulas to compute the test statistic. For example:
Z = ( x̅ – μ0 ) / (σ /√n)
Here:
x̅: sample mean
μ0: population mean
σ: standard deviation
n: sample size
6. Compare with Critical Values or P-Value
Determine whether the test statistic falls within the rejection region or if the p-value is less than the significance level.
7. Make a Decision
If the test statistic lies in the rejection region or p-value < α, reject H₀.
Otherwise, fail to reject H₀.
Checking Directionality in Hypothesis Testing
While hypothesis testing is conducted, determining the directionality of the test is very important. It defines whether you are looking for a change in a specific direction or if there has been a deviation from the baseline. The choice between a one-tailed and a two-tailed test is based on the research question and what you want to prove.
Why Directionality Matters
Focus: A one-tailed test provides higher statistical power for detecting effects in a specified direction.
Breadth: A two-tailed test captures deviations in both directions, making it suitable for non-directional hypotheses.
Example of Importance:
Testing if a drug reduces blood pressure (one-tailed).
Testing if a drug alters blood pressure in any way (two-tailed).
One-Tailed Tests
Definition: Tests for a change in one specific direction.
Types:
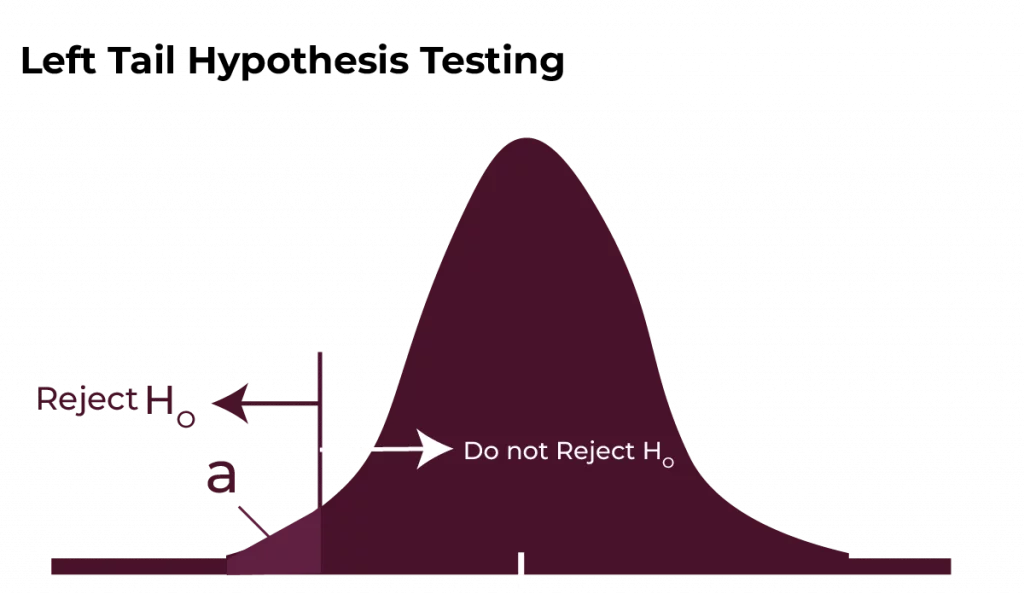
Left-Tailed Test: Checks if a parameter is smaller than the hypothesised value.
Example: Testing if a weight-loss programme reduces weight below the baseline.
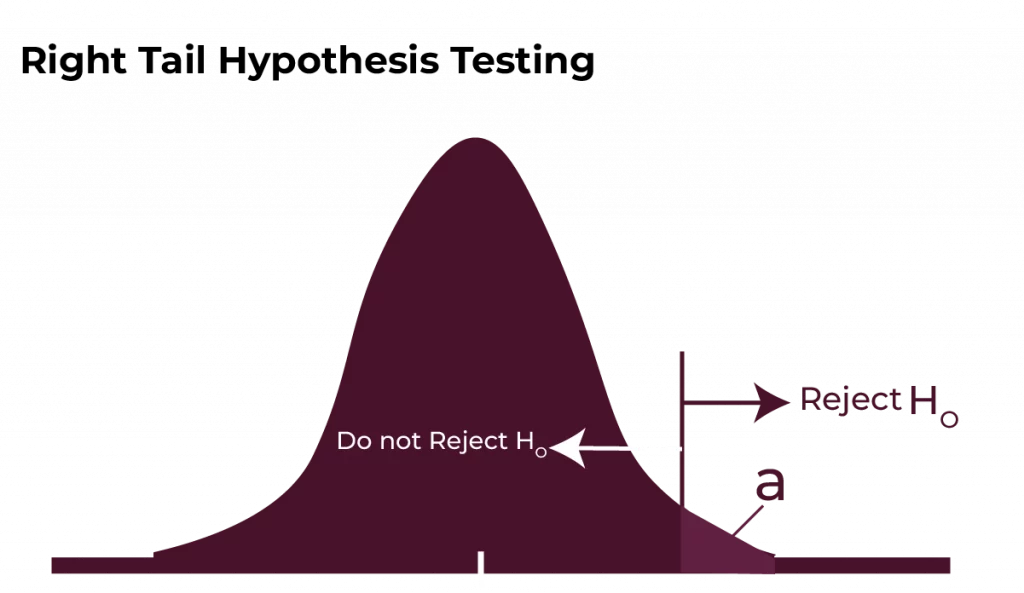
Right-Tailed Test: Checks if a parameter is greater than the hypothesised value.
Example: Testing if a training programme increases productivity above the average.
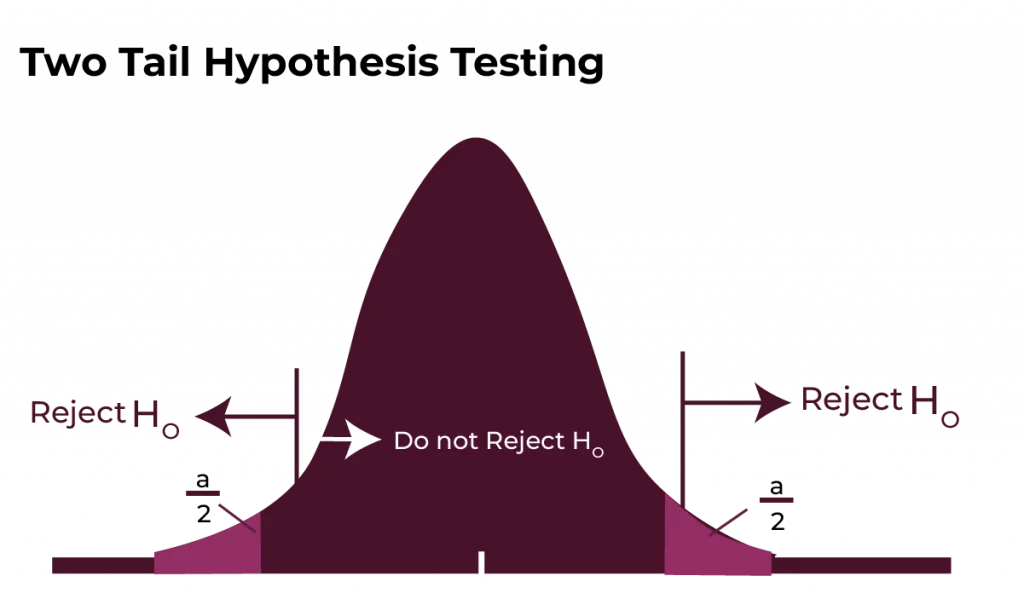
Two-Tailed Tests
Definition: Tests for a change in either direction (greater or smaller).
Example: Evaluating whether the average lifespan of light bulbs differs from the advertised lifespan.
How to Decide on Directionality
Research Objective:
Use a one-tailed test for directional hypotheses (e.g., “increase” or “decrease”).
Use a two-tailed test when the direction doesn’t matter, only the existence of a difference.
Risk of Errors:
A one-tailed test reduces the p-value threshold, increasing the risk of missing effects in the opposite direction.
Exploring the Various Types of Hypothesis Testing in Statistics and Their Applications
Hypothesis testing requires the choice of a correct test. It is about selecting a test that is appropriate to a problem regardless of the data type and size. Here are the main types of hypothesis tests and their applications:
Z-Test: Applicable to Large Samples with Known Standard Deviations
The Z-test is most appropriate in cases when the sample size is reasonable enough (n ≥ 30) and the population standard deviation is well-known.
This involves comparing the sample mean against a population mean to establish if any difference exists.
Application: Determining whether a batch of products meets the desired quality.
Example: Factory-producing LED bulbs state the mean lives will be about 15,000 hours. We have chosen a sample of 50 light bulbs whose mean is 14,800 hours. Now, we use a Z-test to determine whether that difference is statistically significant or not.
Formula:
Z = ( x̅ – μ0 ) / (σ /√n)
Here:
x̅: sample mean
μ0: population mean
σ: standard deviation
n: sample size
T-Test: Handling Small Samples or Unknown Standard Deviations
When the sample size is small (n < 30) or the population standard deviation is unknown, the T-test is the go-to choice.
It compares the sample mean to the population mean or compares two sample means.
Types:
One-Sample T-Test: Tests if the sample mean differs from the population mean.
Two-Sample T-Test: Compares the means of two groups.
Paired T-Test: It is used whenever the same group is measured twice, say, before and after treatment.
Application: Assess if an innovative study technique is effective.
Example: A school implements a new teaching method and tests a class of 20 students before and after using it. A paired T-test can reveal whether the method improved scores.
Formula:
t =( x̅ – μ0 ) / (s /√n)
where,
t = t-score,
x̄ = sample mean
μ0 = population mean,
s = standard deviation of the sample
n = sample size
Chi-Square Test: Ideal for Categorical Data
The Chi-Square test is perfect for examining relationships between categorical variables.
It’s often used in survey data and contingency tables.
Application: Understanding customer preferences across different regions.
Example: A retail store wants to check if customer preferences for product categories differ between urban and rural areas. The Chi-Square test evaluates if these differences are statistically significant.
Formula:
χ2 = ∑(Oij − Eij)^2 / Eij
Terms:
χ2: The Chi-Square statistic
Oij: Observed frequency in the i, j-th cell of a contingency table
Eij: Expected frequency in the i, j-th cell
Eij = (Row Total)×(Column Total)/Grand Total
ANOVA (Analysis of Variance): Comparing Multiple Groups
ANOVA comes into play when comparing the means of three or more groups. It helps identify if at least one group differs significantly.
Application: Testing the performance of sales teams across different regions.
Example: A company measures sales performance in North, South, and West zones. ANOVA determines if the differences are statistically significant.
Common Pitfalls: Understanding Type I and Type II Errors in Statistical Testing
Hypothesis testing in statistics isn’t foolproof. Errors can occur, and understanding them is essential for drawing reliable conclusions.
Type I Error (False Positive)
This error happens when the null hypothesis is rejected even though it’s true.
Impact: Making decisions based on non-existent effects.
Example: Concluding that a new drug is effective when it isn’t. This could lead to unnecessary costs and safety risks.
Type II Error (False Negative)
This occurs when the null hypothesis is not rejected despite being false.
Impact: Missing real effects or relationships.
Example: Overlooking the effectiveness of a marketing campaign that could significantly boost sales.
Set Appropriate Significance Levels: Balancing risks helps avoid extreme outcomes.
Conduct Pilot Studies: Testing on a smaller scale refines assumptions.
By addressing these errors, we enhance the reliability of hypothesis testing in statistics.
Practical Applications of Hypothesis Testing in Various Fields
Let’s look at the application of hypothesis testing in statistics in the real world across different kinds of industries.
Business: Analysing the Impact of Price Reduction on Sales
Businesses often test strategies to optimise revenue.
Scenario: A retailer reduces prices by 10% and observes sales before and after the change across 20 stores.
Hypotheses:
Null Hypothesis (H₀): Price reduction has no impact on sales.
Alternative Hypothesis (H₁): Price reduction increases sales.
Here’s how to run a two-sample t-test for this scenario:
from scipy.stats import ttest_ind
# Data: Sales figures before and after price reduction
before_sales = [500, 520, 510, 530, 525, 540, 515, 530, 510, 525]
after_sales = [550, 560, 580, 600, 590, 610, 570, 600, 575, 580]
# Perform the two-sample t-test
t_stat, p_value = ttest_ind(before_sales, after_sales)
# Output the results
print(f"T-Statistic: {t_stat:.2f}, P-Value: {p_value:.4f}")
# Decision
if p_value < 0.05:
print("Reject the null hypothesis: Price reduction increases sales.")
else:
print("Fail to reject the null hypothesis: No significant impact of price reduction.")
Result
T-Statistic: -8.65
P-Value: 0.0000
Decision: Reject the null hypothesis: Price reduction increases sales.
Healthcare: Evaluating the Efficiency of a New Pharmaceutic Drug
With the introduction of any new pharmaceutical, demonstrating its effects is crucial.
Test Case: A pharmaceutical company conducts research on an anti-hypertensive drug using paired before-and-after measurements of 30 patients.
Hypotheses:
H₀ (Null Hypothesis): The drug has no effect on blood pressure.
H₁ (Alternative Hypothesis): The medicine lowers the blood pressure.
A paired t-test is used because the same patients are measured before and after treatment.
The following outlines the methodology for conducting this test utilising Python:
from scipy.stats import ttest_rel
# Data: Blood pressure levels before and after treatment
before_treatment = [150, 145, 140, 155, 160, 165, 150, 148, 142, 155]
after_treatment = [140, 135, 132, 145, 150, 155, 145, 140, 138, 148]
# Perform the paired t-test
t_stat, p_value = ttest_rel(before_treatment, after_treatment)
# Output the results
print(f"T-Statistic: {t_stat:.2f}, P-Value: {p_value:.4f}")
# Decision
if p_value < 0.05:
print("Reject the null hypothesis: The drug is effective.")
else:
print("Fail to reject the null hypothesis: Insufficient evidence to conclude the drug's effectiveness.")
Result:
T-Statistic: 11.52
P-Value: 0.0000
Decision: Reject the null hypothesis: The drug is effective.
Education: Evaluating the Success of a New Teaching Method
In education, testing teaching strategies can help improve student outcomes.
Scenario: A new teaching method is introduced to improve exam scores. Test scores of a group of 25 students are recorded before and after adopting the method.
Hypotheses:
Null Hypothesis (H₀): The teaching method does not affect student scores.
Alternative Hypothesis (H₁): The teaching method improves student scores.
A paired t-test is used:
from scipy.stats import ttest_rel
# Data: Test scores before and after the new method
before_scores = [60, 62, 65, 58, 63, 61, 59, 62, 64, 60]
after_scores = [70, 72, 75, 68, 73, 71, 69, 72, 74, 70]
# Perform the paired t-test
t_stat, p_value = ttest_rel(before_scores, after_scores)
# Output the results
print(f"T-Statistic: {t_stat:.2f}, P-Value: {p_value:.4f}")
# Decision
if p_value < 0.05:
print("Reject the null hypothesis: The new teaching method is effective.")
else:
print("Fail to reject the null hypothesis: Insufficient evidence to conclude effectiveness.")
Result:
T-Statistic: -inf
P-Value:0000
Reject the null hypothesis: The new teaching method is effective.
Coin Flip Example: Testing Fairness
Even simple experiments benefit from hypothesis testing.
Scenario: Testing if a coin is biased.
Null Hypothesis: The coin is fair (50% heads, 50% tails).
Method: Test the distribution of 100 coin tosses using a Chi-Square test.
Outcome: In case the p-value>0.05, then the coin is said to be fair.
Tools for the Practical Application of Hypothesis Testing in Statistics
Performing hypothesis testing in statistics requires the right tools to streamline the process, especially when dealing with large datasets. These tools not only simplify calculations but also enhance accuracy and speed.
Here’s a list of popular tools:
Python:
Python libraries like scipy.stats offer robust functions for hypothesis testing.
From t-tests to ANOVA, it handles a wide range of statistical tests.
Example: Testing the average height of a group using a one-sample t-test:
R:
Known for its statistical capabilities, R is a go-to tool for researchers.
Functions like t.test() and chisq.test() makes hypothesis testing simple.
Excel:
With built-in formulas and add-ins like Analysis ToolPak, Excel is a beginner-friendly choice.
It’s best suited for smaller datasets or when visualisation is key.
SPSS:
A user-friendly tool designed for non-technical users.
Its drag-and-drop interface makes statistical analysis accessible to all.
MATLAB:
Ideal for advanced users, MATLAB provides extensive features for complex statistical modelling.
Choosing the Right Tool
For simplicity and flexibility: Python or Excel.
For visualisation: SPSS or Excel.
For advanced research: R or MATLAB.
Challenges and Limitations in Applying Hypothesis Testing
While hypothesis testing in statistics is a powerful tool, it’s not without challenges. Understanding these limitations ensures better application and interpretation.
Dependency on Sample Quality
Hypothesis testing relies heavily on the quality of the sample.
Poorly collected or biased data can lead to misleading conclusions.
Risk of Errors
Type I Error: Incorrectly rejecting the null hypothesis.
Type II Error: Failing to reject a false null hypothesis.
Balancing the significance level helps reduce these risks, but errors can still occur.
Complexity of Real-World Scenarios
Simplified assumptions, like normal distribution or independence of data points, may not hold true in real-world situations.
For instance, testing customer behaviour in a retail setting might involve multiple overlapping factors, complicating analysis.
Misinterpretation of Results
A low p-value doesn’t always mean the null hypothesis is false.
Results should be interpreted in context, considering factors like sample size and experimental design.
How to Overcome These Challenges
Pilot Studies: Conducting smaller tests can refine hypotheses and methods.
Cross-Validation: Using multiple datasets ensures robustness.
Expert Review: Consulting with statisticians can clarify doubts.
Conclusion
Hypothesis testing in statistics has been an important tool for proving assumptions and making informed decisions by industries. It connects raw data to actionable insights, making sure all decision-making is evidence-based.
Understanding the basic concepts of null and alternative hypotheses, significance levels, and types of errors makes navigating the complexities of real-world data quite manageable.
Tools like Python and techniques such as t-tests and ANOVA simplify the process for diverse applications, from evaluating medical treatments to optimising business strategies.
Through structured steps and careful interpretation, hypothesis testing in statistics empowers data-driven approaches, fostering accuracy and reliability in outcomes while addressing challenges effectively.
To deepen your expertise in these techniques and more, consider the Accelerator Program in Business Analytics & Data Science by Hero Vired with edX and Harvard University. This program provides hands-on training and industry insights, empowering you to excel in analytics and data science.
FAQs
What is the primary goal of hypothesis testing?
The key objective of hypothesis testing is to determine whether enough evidence exists to support or deny a statement about a population parameter.
How would I select the appropriate test for hypothesis testing?
It depends on the type of data and sample size. For example:
Large samples: Z-test.
Small samples: T-test.
Categorical data: Chi-Square test.
What is a p-value in hypothesis testing?
The strength of evidence against the null hypothesis is signified by a p-value. A smaller p-value, for example, less than 0.05, indicates a more reasonable ground for rejection.
What tools can be used for hypothesis testing?
Popular tools include Python, R, Excel, SPSS, and MATLAB. Each has its strengths depending on your expertise and dataset size.
How can I minimise errors in hypothesis testing?
Use larger sample sizes to reduce variability.
Choose an appropriate significance level (commonly 0.05).
Validate results through repeated testing or additional datasets.
Hero Vired is a leading LearnTech company dedicated to offering cutting-edge programs in collaboration with top-tier global institutions. As part of the esteemed Hero Group, we are committed to revolutionizing the skill development landscape in India. Our programs, delivered by industry experts, are designed to empower professionals and students with the skills they need to thrive in today’s competitive job market.
