Hierarchical clustering is one of the most popular unsupervised machine learning techniques, especially for revealing patterns, structures, or groups within data. Unlike other clustering algorithms like K-means, hierarchical clustering does not require a predefined number of clusters. This, thus, makes it a highly adaptive approach to data discovery, particularly in situations where the underlying number of clusters is not known a priori.
In this article, we will learn about hierarchical clustering in detail. We will examine its functionality, the hierarchical clustering types, purpose, benefits, drawbacks, and specific real-life examples, as well as its execution in Python. By the time you are through this article, you will be looking at hierarchical clustering with a good understanding of where it gets applied in machine learning.
What is Hierarchical Clustering?
Hierarchical clustering is an unsupervised ML algorithm of cluster analysis that focuses on creating several clusters that can be shown using a tree-like diagram called a dendrogram. It partitions the data into nested clusters, which form a tree. Hierarchical cluster analysis helps in locating tendencies and relationships between data sets. A dendrogram displays the results, illustrating the distance relationship among clusters. There are two different types of hierarchical clustering: agglomerative and divisive. Basic clustering methods are characterized by condensation, the fusion of similar data points.
In contrast, common agglomerative clustering modeWhen the structure or the number of clusters is unknown, this clustering method is advantageous as it produces a hierarchy that can be separated at any point, yielding the number of clusters required. Hierarchical cluster analysis (HCA), also known as hierarchical clustering,g is a clustering method that creates clusters of a collection of objects as groups with hierarchy elements without putting them in a linear arrangement. Hierarchical clustering methods are used in many fields- biology, image analysis, social sciences, etc., to analyze and discern the structure and relationships.
Get curriculum highlights, career paths, industry insights and accelerate your data science journey.
Download brochure
Hierarchical Clustering Algorithm
Hierarchical clustering uses a technique in which the elements of a dissimilarity matrix are used to determine the level of per cluster merging or dividing is similarity, which refers to the distance between two data points according to some linkage criteria. A dissimilarity matrix contains the values that include:
The distance, and
A linkage clustering criterion
Distance Measures in Hierarchical Clustering
The hierarchical clustering technique requires a distance or dissimilarity measure between data points that must be clustered. For hierarchical clustering purposes, several such distance metrics can be employed:
1. Euclidean Distance: The Euclidean distance is the most common distance measure in hierarchical clustering. This measure determines the distance between two points by a straight line in a multi-dimensional space.
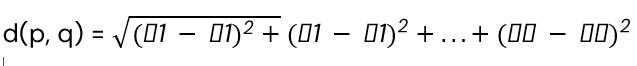
2. Manhattan Distance: The Manhattan distance, also known as the city block distance, calculates the absolute sum of the variations between two sites on a line that resembles a grid. The Manhattan distance for points p and q can be found using:
d(p, q) = |p1 – q1| + |p2 – q2| + … + |pn – qn|
3. Cosine Similarity: Cosine similarity evaluates how similar two vectors are by measuring the angle between them. It is frequently used when working with high-dimensional data, such as text data represented by TF-IDF vectors. The following formula calculates cosine similarity S between vectors A and B:
S(A, B) = , here, Where A⋅B is the dot product of the vectors.
Linkage Methods in Hierarchical Clustering
Single Linkage: Also known as nearest point linkage, this method considers the distance between two clusters, containing at least one common point from each cluster, as the minimum distance connecting all single pairs of the cluster’s points.
Complete Linkage: Complete linkage (or farthest point linkage) defines the distance between two clusters as the maximum distance between a point in one cluster and a point in the other. This tends to produce compact spherical clusters.
Average Linkage: Average linkage defines the distance between any two clusters regarding the arithmetic mean distances of all the points within each cluster. It is a compromise between single and complete linkage.
Ward’s Linkage: This method minimizes the variance of each cluster. It merges clusters so that the total within-cluster variance does not rise appreciably above what it was following the optimal solution at that level of clustering. Often, it produces well-separated clusters, and for this reason, it is commonly used in practice.
The hierarchical clustering is categorized into two types:
Agglomerative Clustering
Divisive Clustering
Agglomerative Clustering
A hierarchical agglomerative clustering algorithm is a bottom-up approach where each data point is initially considered a single cluster. These clusters are then sequentially merged with others, starting from smaller to larger ones, until the last single cluster, or benchmark conditions, is reached. The number of clusters does not need to be predetermined using this clustering procedure.
Characteristics
Agglomerative is quite slow and inappropriate for larger data sets because it performs many merging and distance computations.
The procedure is deterministic; given the same dataset and linkage options, the output is always the same hierarchy of organization.
Agglomerative Clustering Algorithm
Initialization:
Start with n clusters, where each data point is its cluster.
Compute a distance matrix for all data points.
Repeat:
Find the two clusters with the smallest distance in the distance matrix.
Merge these two clusters into a new cluster.
Using a linkage criterion (e.g., single-linkage, complete-linkage), update the distance matrix to reflect the distance between the new cluster and all other clusters.
Stop:
This step is continued until the single cluster is achieved or the required number of clusters has been reached.
linkage_criterion – Method for calculating inter-cluster distances (e.g., single, complete, average)
Output: Hierarchical cluster tree
Initialize:
Create n clusters, each containing one data point
Compute the distance matrix for all points
While (number of clusters > 1):
Find the two closest clusters (Ci, Cj) based on the distance matrix
Merge clusters Ci and Cj into a new cluster C_new
Update the distance matrix using the linkage_criterion
Remove Ci and Cj from the list of clusters
Add C_new to the list of clusters
Return: Hierarchical cluster tree
Example:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.Datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
# random data
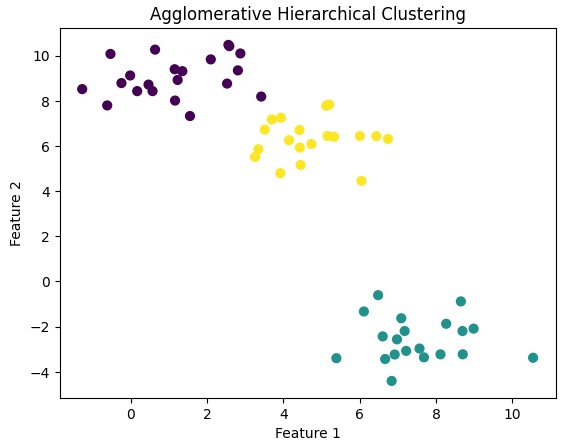
X, _ = make_blobs(n_samples=60, centers=3, random_state=32)
# Agglomerative
agg_clustering = AgglomerativeClustering(n_clusters=3, linkage='ward')
y_pred = agg_clustering.fit_predict(X)
# Plot the clustered data
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=40)
plt.title("Agglomerative Hierarchical Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
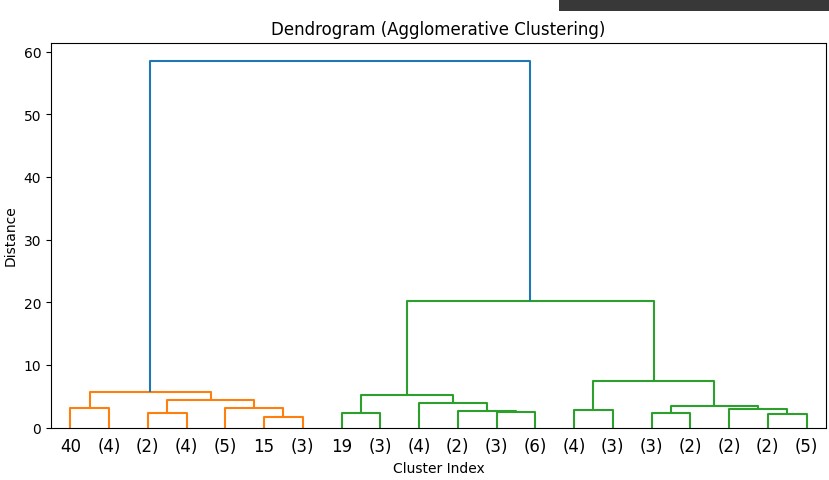
# Dendrogram
linked = linkage(X, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(linked, truncate_mode='lastp', p=20)
plt.title("Dendrogram (Agglomerative Clustering)")
plt.xlabel("Cluster Index")
plt.ylabel("Distance")
plt.show()
Output:
Divisive Clustering
Divisive hierarchical clustering is a top-down approach. In divisive clustering, all data points are initially in a single cluster. This cluster is successively divided into smaller clusters until all the data points are individually clustered and certain stopping criteria are achieved. Divisive clustering is the opposite of agglomerative clustering.
Characteristics
During the act of division, all existing potential splits of a cluster have to be considered and evaluated; hence, divisive clustering incurs a high computational burden, which is more severe if the datasets are large.
It is usually about other clustering techniques that try to provide an answer to how to split a cluster, such as PCA or graph partitioning.
In most instances, managing users using this method does not fit the ideal case or model. It is not very frequently applied compared to agglomerative clustering methods due to the great computation it requires.
Divisive Clustering Algorithm
Initialization
Start with all data points grouped into a single cluster
Repeat:
Select the cluster to split.
Use a highlighting criterion (e.g., maximize inter-cluster distance or minimize intra-cluster distance) to divide the cluster into two sub-clusters.
Reassign points to the sub-clusters based on the criterion.
Stop:
Repeat until all points form their clusters or the desired number of clusters is reached.
splitting_criterion – Method for splitting clusters (e.g., PCA, distance-based)
Output: Hierarchical cluster tree
Initialize:
Start with a single cluster containing all data points
Cluster_list = [All data points]
While (number of clusters < n or stopping condition not met):
Select the cluster C from Cluster_list to split
Split C into two sub-clusters (C1, C2) based on splitting_criterion
Remove C from Cluster_list
Add C1 and C2 to Cluster_list
Return: Hierarchical cluster tree
Example:
from sklearn.datasets import make_blobs
from sklearn.metrics import pairwise_distances
import numpy as np
import matplotlib.pyplot as plt
# Generate random data
X, _ = make_blobs(n_samples=50, centers=3, random_state=32)
def divisive_clustering(data, max_clusters):
clusters = [list(range(len(data)))] # Start with one cluster containing all points
final_clusters = []
while len(clusters) < max_clusters:
# Select the largest cluster to split
largest_cluster = max(clusters, key=len)
clusters.remove(largest_cluster)
# Compute pairwise distances within the cluster
distances = pairwise_distances(data[largest_cluster])
# Find the farthest two points in the cluster to start the split
idx1, idx2 = np.unravel_index(np.argmax(distances), distances.shape)
point1, point2 = largest_cluster[idx1], largest_cluster[idx2]
# Assign points to two new clusters
cluster1, cluster2 = [], []
for idx in largest_cluster:
if np.linalg.norm(data[idx] - data[point1]) < np.linalg.norm(data[idx] - data[point2]):
cluster1.append(idx)
else:
cluster2.append(idx)
# Add the new clusters
clusters.append(cluster1)
clusters.append(cluster2)
# Convert cluster indices to data points
final_clusters = [data[cluster] for cluster in clusters]
return final_clusters
# Perform divisive clustering
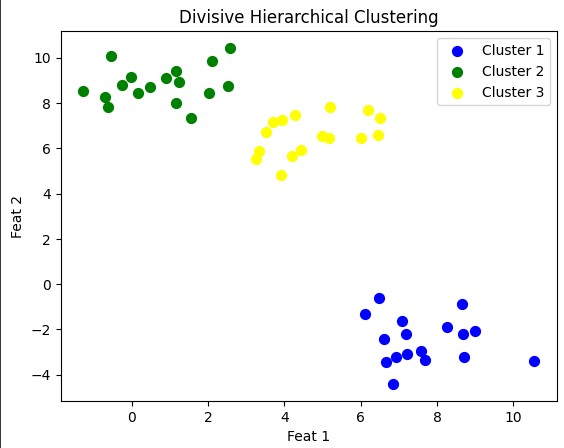
max_clusters = 3
clusters = divisive_clustering(X, max_clusters)
# Plot the clusters
colors = ['blue', 'green', 'yellow']
for i, cluster in enumerate(clusters):
plt.scatter(cluster[:, 0], cluster[:, 1], color=colors[i], s=50, label=f'Cluster {i+1}')
plt.title("Divisive Hierarchical Clustering")
plt.xlabel("Feat 1")
plt.ylabel("Feat 2")
plt.legend()
plt.show()
Output:
Hierarchical Clustering vs K-means Clustering
In machine learning, two popular clustering methods are K-Means Clustering and Hierarchical Clustering. Here is a comparison of both on the major factors:
Approach: Hierarchical clustering follows the strategy of creating a tree (dendrogram) by either successively joining (agglomerative) or dividing (divisive) clusters. At the same time, K-Means repeatedly updates centroid locations to divide a data set into k subgroups.
Cluster Shape: Hierarchical clustering has no restrictions on the scope or compactness of clusters, whereas K-Means defines the cluster as spherical and is not too effective with non-regular-shaped clusters.
Distance Metrics: Several linkage metrics (single, complete, average, etc.) can be employed when implementing hierarchical clustering, while K-Means are restricted to Euclidean distance.
Scalability: Due to its algorithmic time complexity, O(k⋅n⋅i), K-means is appropriate for large data sets. The complexity of hierarchical clustering is O(n2 log n), which is greater than K-means’ complexity due to the step requiring the calculation of the instance matrix.
Flexibility: The specific number of clusters that must be set or estimated before the algorithm begins, unlike K-Means, which requires k to be determined before execution of the algorithm.
Various disciplines benefit from hierarchical clustering, including:
Biology: Genomics and bioinformatics frequently employ it to cluster genes demonstrating similar expression patterns or to classify organisms based on their genetic similarity.
Marketing: Within customer segmentation, hierarchical clustering provides insights into customers with similar buying patterns, improving the focus of marketing campaigns.
Document Clustering: In information retrieval and natural language processing, hierarchical clustering finds applications to organize documents with similar content or articles on the same topic.
Image Segmentation and Processing: It conserves the purpose of partitioning images into regions with similar attribute values like color or texture. In-text image recognition, hierarchical clustering is utilized to classify handwritten characters according to their shapes.
Benefits and Challenges of Hierarchical Clustering
Benefits
No, Unlike K-means, there is a pre-definition of clusters: It does not require the user to predetermine the number of clusters that produce a dendrogram. It is possible to view the clustering in greater detail and see one cluster’s composition more vividly and how it relates to other clusters.
Works well with small datasets: For smaller datasets, where computation may not become a problem, this method can work well and give highly accurate results.
Can handle non-globular clusters: Unlike K-means, which assume spherical clusters, the method can find clusters of different shapes.
Challenges
Not easily applicable to large datasets: Owing to the computational burden, hierarchical clustering may not be suitable for large datasets.
Computational complexity: For large datasets, hierarchical clustering can be computationally costly. When n is the number of data points, the temporal complexity is usually O(n^3).
Sensitive to noise and outliers: WheOutliersn significantly impacts the clustering findings.
Conclusion
Hierarchical clustering overcomes many of the limitations of other clustering approaches due to its strength in developing clusters. It offers important insights into the relationships between data sets by creating a hierarchy of clusters. Even though it can be computationally costly, it is a popular option in many applications due to its capacity to generate a complex hierarchy and the freedom to choose the number of clusters.
Hierarchical clustering is one of the methods that allows for discovering hidden patterns, regardless of the domain in which you are working: biological data, customers’ behavior, or even text data. With this certificate in machine learning-powered program learning-powering artificial intelligence and Machine Learning Powered by Herovired, learn machine learning and gain a professional knowledge certificate.
FAQs
What is hierarchical clustering?
Hierarchical clustering is a relatively simple machine-learning technique employed to classify a dataset into a hierarchy of clusters of elements. They are of two types: agglomerative (combining clusters, letting the starting point be the individual points) or divisive (letting all points be in one cluster at the beginning and splitting the clusters).
What distinguishes divisive hierarchical clustering from agglomerative clustering?
Agglomerative clustering is a ‘bottom-up that eats each point as a distinct cluster connected after multiple rounds. Divisive clustering is the opposite, as it can also be termed 'top-down,' where all cluster points are housed within one mass, and portions are taken from that mass.
What are the linkage methods in hierarchical clustering?
The Linkage algorithms determine the distance between clusters during merging or splitting. Common linkage methods include Ward's approach (minimizing variance), average linkage, single linkage (minimum distance), and complete linkage (maximum distance).
What is the most dependable hierarchical clustering technique?
Because of its ease of use and efficiency, the agglomerative clustering approach is the most dependable hierarchical clustering technique.
What is K-means clustering?
K-means clustering is an unsupervised machine learning algorithm that utilizes several clusters in its operations. It is common in dataset partitioning types because it classifies members into distinct groups determined by the distance between the centroids.
Hero Vired is a leading LearnTech company dedicated to offering cutting-edge programs in collaboration with top-tier global institutions. As part of the esteemed Hero Group, we are committed to revolutionizing the skill development landscape in India. Our programs, delivered by industry experts, are designed to empower professionals and students with the skills they need to thrive in today’s competitive job market.
