Difference Between Linear and Non-Linear Data Structures

Updated on September 24, 2024

Article Outline

Do you ever ask yourself why the appropriate choice of data structure is crucial while coding or developing software? More often than not, we face performance problems, memory wastage, and slow programs because of poor choice of data structure. Understanding the difference between linear and non-linear data structures will solve most of these problems.

The data structure is the backbone of programming; it helps one arrange and manage data effectively. No system would mean even the best algorithm will not function well. It is like saving books; do we want them all in a pile or put on shelves by genre? The same thing also happens with programming.

Let’s have a look at the two most used methods for data storage and management: linear and non-linear data structures. Understanding their differences in depth will make us better decision-makers in choosing what to use and when, hence making our programs more efficient and easier to maintain.

What is a Linear Data Structure? Characteristics and Key Concepts

Linear data structures are like an ordered queue of people waiting in the movie theatre for ticket acquisition. Each person is connected to the next person and has to follow an identical path. In the linear data structure, data elements are arranged in a sequence one after the other. It’s pretty simple at times and really easy to follow, but sometimes, that simplicity comes at the cost of flexibility.

Here are the basic features of linear data structures:

Single-level organisation: Data is arranged in a straight line that makes it easy to access.
Simple traversal: We can reach each element in one pass from the beginning to the end.
Efficient for small, simple data sets: Ideal when we do not need to manage complex relations between elements.

We use linear structures to ensure the order in which data will arrive. But remember, linear data structures might be inefficient if the dataset reaches a certain size: it may increase memory waste or reduce performance.

Get curriculum highlights, career paths, industry insights and accelerate your technology journey.

Download brochure

Exploring Non-Linear Data Structures and Their Defining Features

Suppose we had a family tree instead of a ticket line. Each person in the tree is connected, but not in a straight line; it is accompanied by ramifications, relationships, and multiple ways that one can reach some particular person from any other person in the tree. This is exactly how non-linear data structures work.

Non-linear data structures allow us to store data that doesn’t come off a single sequence. Instead, the elements are connected at different levels, forming complex hierarchies or networks.

Some important properties of non-linear data structures are:

Multilevel organisation: Data is not aligned in a straight line but is kept spread out in the form of branches or nodes.
Complex traversal: To access all elements may require several passes through different paths.
Ideal for handling complex relationships: Perfect when we need to represent systems like family trees, social networks or computer file systems.

Although they are harder to understand, they are very convenient representations of relationships that may exist between data elements, not mere sequences.

Dive into Common Types of Linear Data Structures with Unique Examples

Linear data structures are the bread and butter of programming. We use them for everything from managing lists of items to controlling the flow of tasks. Let’s break down a few of the most common types and how they work.

Arrays: The Simple Collection of Ordered Elements

An array is like a row of lockers, where each locker has a definite number and holds one thing. In programming, we use an array to store multiple elements of the same kind in a single, contiguous block of memory. Each element is accessed by its index starting at 0.

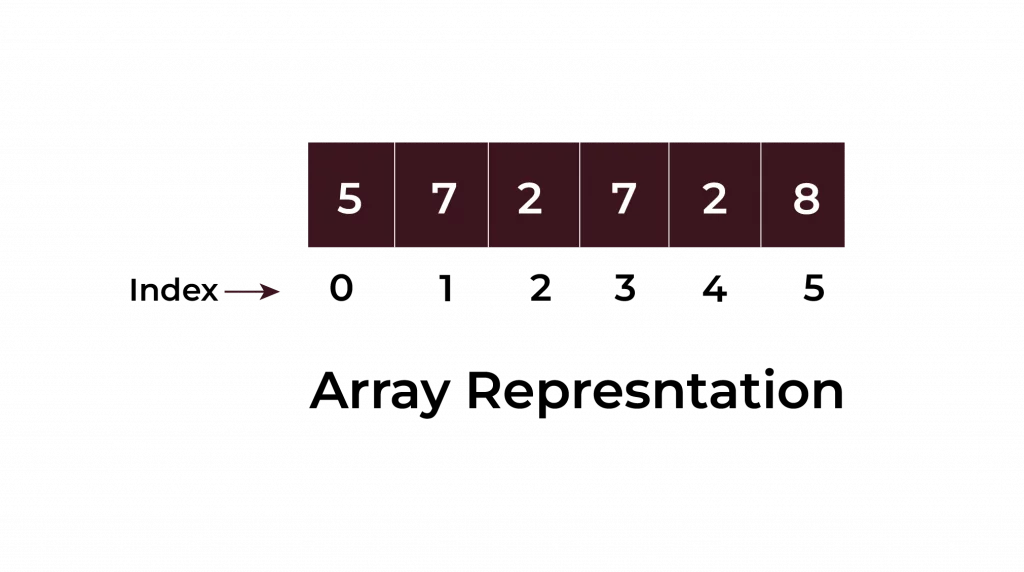
Arrays representation

Example: Let’s create an array that stores the ages of students in a class, taking input from the user:

students = int(input("Enter the number of students: "))

ages = []

for i in range(students):

age = int(input(f"Enter age of student {i+1}: "))

ages.append(age)

print("The ages of the students are: ", ages)

Output:

Enter the number of students: 5

Enter age of student 1: 24

Enter age of student 2: 28

Enter age of student 3: 28

Enter age of student 4: 25

Enter age of student 5: 26

The ages of the students are: [24, 28, 28, 25, 26]

This is a simple array that allows us to manage a list of student ages without creating multiple variables. It’s efficient, easy to understand, and great for basic tasks.

Stack: Using the LIFO Principle for Managing Data

A stack works just like a pile of plates in the kitchen. We always place the last plate on top and take the top one first. This is known as the Last In, First Out (LIFO) principle.

We use stacks in programming when we need to manage items in a last-to-first order.

Example: Let’s simulate a stack of books where we can add and remove books as needed:

stack = []

def push(book):

stack.append(book)

print(f"Book '{book}' added to the stack")

def pop():

if not stack:

print("Stack is empty")

else:

removed_book = stack.pop()

print(f"Book '{removed_book}' removed from the stack")

push("Data Structures")

push("Algorithms")

pop()

pop()

Output:

Book 'Data Structures' added to the stack

Book 'Algorithms' added to the stack

Book 'Algorithms' removed from the stack

Book 'Data Structures' removed from the stack

This stack helps us manage tasks like undo operations in text editors or managing function calls in recursion.

Queue: Leveraging the FIFO Principle in Data Management

Queues work like a real-life queue at a bank. The first person in line is the first one served. This is the First In, First Out (FIFO) principle.

We use queues in programming when tasks need to be processed in the order they arrive.

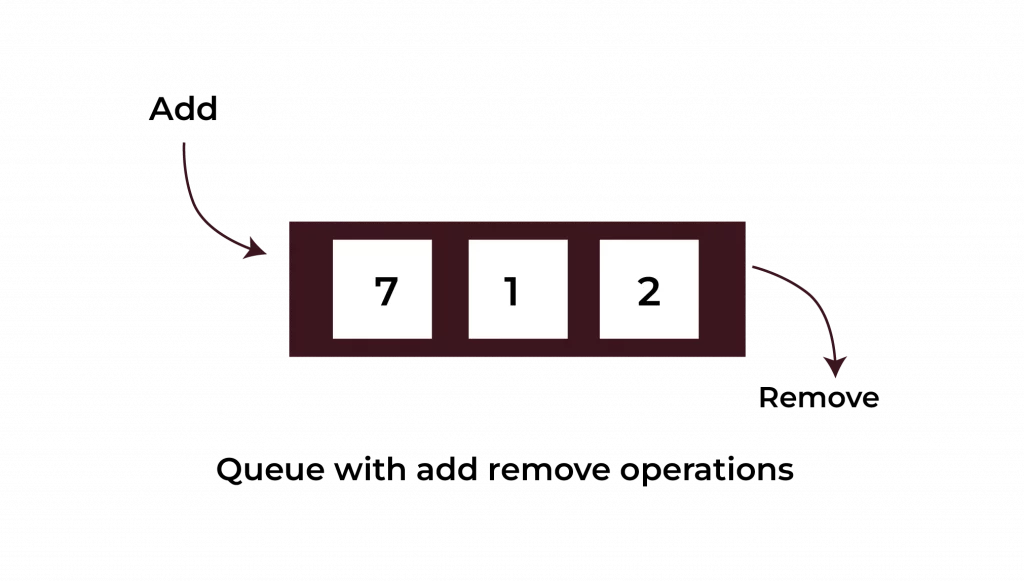
LIFO Principle for Managing Data

Example: Here’s a program that simulates a queue of customers waiting at a store counter:

from collections import deque

queue = deque()

def enqueue(customer):

queue.append(customer)

print(f"Customer '{customer}' added to the queue")

def dequeue():

if not queue:

print("Queue is empty")

else:

served_customer = queue.popleft()

print(f"Customer '{served_customer}' served")

enqueue("Ravi")

enqueue("Ayesha")

dequeue()

dequeue()

Output:

Customer 'Ravi' added to the queue

Customer 'Ayesha' added to the queue

Customer 'Ravi' served

Customer 'Ayesha' served

Queues are useful for managing tasks like printer job queues or customer support systems, where requests are handled in the order they arrive.

Linked Lists: Storing Data in Nodes

A linked list is a bit more complex. Each element, or node, contains both the data and a reference (or link) to the next node in the list. Think of it like a scavenger hunt, where each clue leads to the next.

Linked Lists

Example: Here’s a simple program to create and display a linked list of students:

class Node:

def __init__(self, data):

self.data = data

self.next = None

 

class LinkedList:

def __init__(self):

self.head = None

 

def insert(self, data):

new_node = Node(data)

new_node.next = self.head

self.head = new_node

 

def display(self):

current = self.head

while current:

print(current.data)

current = current.next

 

# Creating linked list and inserting student names

students = LinkedList()

students.insert("Anjali")

students.insert("Rahul")

students.insert("Kavita")

 

students.display()

Output:

Kavita

Rahul

Anjali

Linked lists are helpful when the size of the data can change frequently, like a playlist where songs can be added or removed dynamically.

Types of Non-Linear Data Structures with Unique Examples and Applications

Non-linear data structures have been intimidating, especially when we are at the mountain-top-one glance. We often wonder how to be efficient with complex connections within the data, especially when things don’t flow in a straight line. This is where non-linear structures come in handy and allow us to work with data that doesn’t follow a neat, ordered list.

These are non-linear data structures. Once sequences get too simple, they are no longer enough. In a web, not a line, the elements are tied. This allows more flexibility in modelling complex relationships.

Let’s now discuss some of the common types along with their unique uses.

Trees: Organising Data in a Hierarchical Manner

Consider a family tree: It’s a fantastic example of a tree data structure. You go all the way back to one person- the root node- and then branch out for every generation after that. In a tree data structure, data is structured hierarchically, with each element called a “node”-connected to other nodes in a parent-to-child relationship.

For instance, in a binary tree, each node will have at most two children. A binary search tree, which is a special case of a binary tree, finds wide usage in applications that use the search engines. For each node, the left child needs to have nodes smaller than the parent, and the right child should contain nodes greater than the parent.

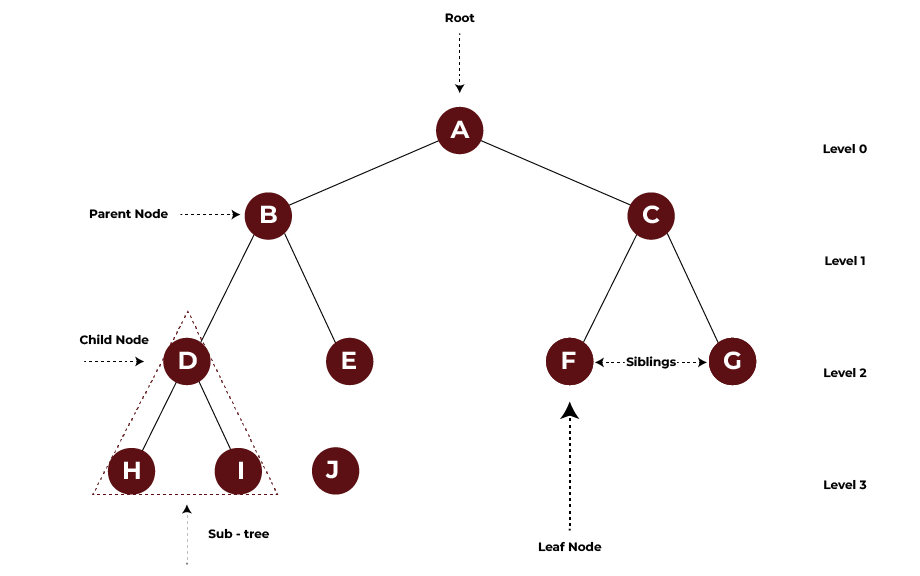
Tree structure

Here is a very simple Python program which asks for the number from the user and inserts the nodes into the binary search tree:

class Node:

def __init__(self, data):

self.data = data

self.left = None

self.right = None

def insert(root, key):

if root is None:

return Node(key)

if key < root.data:

root.left = insert(root.left, key)

else:

root.right = insert(root.right, key)

return root

def inorder(root):

if root:

inorder(root.left)

print(root.data, end=" ")

inorder(root.right)

root = None

values = [int(x) for x in input("Enter values to insert into BST: ").split()]

for value in values:

root = insert(root, value)

print("In-order traversal of the tree:")

inorder(root)

Output:

Enter values to insert into BST: 190

In-order traversal of the tree:

190

In this program, we make a binary search tree from user input and then print out the tree through in-order traversal. Because of the nature of a tree, you can seek values in a tree way faster than you can seek values in a list.

Applications of tree structures:

File systems: Folders and files in an operating system are in a hierarchical format.
Decision-making: Tree structures with only two child nodes by each node are used in machine learning to make predictions about data.
Database indexing: Trees such as the B-trees are useful in efficient searching and retrieval of databases

Also Read: Difference Between Binary Tree and Binary Search Tree

Graphs: Representing Complex Relationships Between Data Elements

Unlike trees, graphs are much more flexible and do not establish a strict parent-child relationship. Instead of a hierarchy from parent to child, nodes known as vertices connect through edges, and one node can connect to multiple nodes. It would be natural to model networks like roads between cities or connections on a website such as Facebook using graphs.

For example, consider a small social network. We can represent any person as a node. Connections between people (friends) are edges.

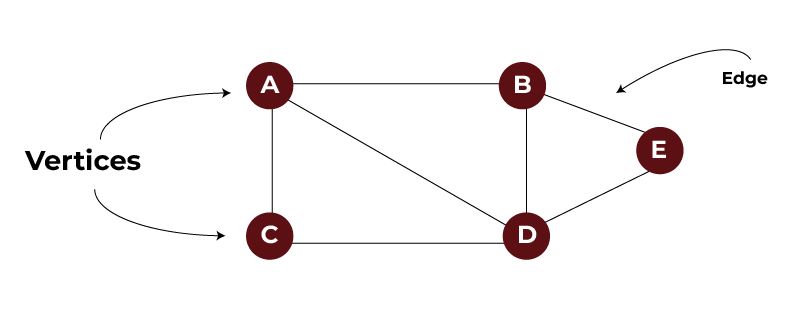
Graphs: Representing Complex Relationships

Let’s see an example of a Python program that constructs a graph and shows the connections in it.

class Graph:

def __init__(self):

self.graph = {} 

def add_edge(self, node, neighbour):

if node not in self.graph:

self.graph[node] = []

self.graph[node].append(neighbour)

 

def display_graph(self):

for node in self.graph:

print(f"{node} -> {', '.join(self.graph[node])}") 

g = Graph()

edges = [("Ravi", "Sita"), ("Ravi", "Raj"), ("Sita", "Raj"), ("Raj", "Mohan")]

for edge in edges:

g.add_edge(*edge) 

print("Graph connections:")

g.display_graph()

Output:

Graph connections:

Ravi -> Sita, Raj

Sita -> Raj

Raj -> Mohan

In the following graph, we have four people: Ravi, Sita, Raj, and Mohan. The above program shows how they are connected.

Applications of graphs:

Social networks: Facebook, LinkedIn, and Instagram all use graphs to show their user connections.
Navigation systems: Google Maps uses graphs to model roads and find the shortest path between two points.
Telecommunications: Telephone networks are modelled as graphs to enable efficient routing of calls.

Linear vs. Non-Linear Data Structures

We have discussed basic ideas of both linear and non-linear data structures. Now, let’s observe how these stack up with one another.

Linear Data Arrangement vs. Hierarchical Data Arrangement

Linear: Data are arranged in a series that is one after the other.
Non-linear: Data are spread across several levels or nodes, and there is no set order.

Traversal: Single vs. Multiple Traversal Methods

Linear: All data can be traversed in one go since everything travels along a straight line.
Non-linear: In most cases, traversal of all the data necessitates passes several times over, especially for structures like trees and graphs.

Levels of Organisation: One-Level vs. Multi-Level Structures

Linear: All the elements reside at just one level.
Non-linear: Data is arranged on several dimensions, so the components have intricate interactions.

Memory Utilisation: Linearity vs. Non-linearity Efficiency

Linear: In most cases less efficient regarding space since the area allocated is whether it is utilised or not.
Non-linear: It is much more efficient because memory only becomes used when it is needed.

Implementation Complexity: Simple vs. Complicated

Linear: In most ways, fairly simple to implement, yet this tends to increase in inefficiency as larger or more complex data sets are involved.
Non-linear: Not that easy to design but provides extensibility and scalability for complex applications.

Time Complexity: How Input Size Impacts Performance

Linear: The time complexity is linear to the data size.
Non-linear: Time complexity tends to be constant because these structures are well-built in such a way that they are resistant to large datasets.

Memory Utilisation in Linear and Non-Linear Data Structures: How Resource-Intensive Are They?

Perhaps one of the greater efficiencies of the non-linear data structures is that they can make a better usage of memory space.

For linear data structure, we have to allocate the space for each element. Even if we are not making full use of that, we have to do so. For example, in an array, its size is fixed when it is created. This can consume much of the space.

On the other hand, non-linear structures, such as trees and graphs, allocate memory dynamically. They grow as we add more data, making them so much more memory-efficient in dealing with large or complex datasets.

Consider a linked list compared to an array. In a linked list, memory is allocated node-by-node, while in arrays, memory is pre-allocated in a fixed block. This attribute of non-linear data structures makes them more preferably used in dynamically growing data that may be unpredictable.

Important points to remember:

Linear structures: An amount of memory is pre-allocated for required space, which may be wasted.
Non-linear structures: Memory is allocated at run-time; thus, the available spaces are not wasted.

Also Read: Difference Between Prims And Kruskal Algorithm

Time Complexity and Performance: Difference Between Linear and Non-Linear Data Structure

When one is building software, the biggest concern is always performance. Nobody likes to have an application running slowly. So, which is the best, the linear one or the non-linear data structure? It all depends on the size and complexity of your data.

The growth of the size of data increases the time complexity of linear data structures like arrays or linked lists. When an item needs to be found, then every element needs to be looked into. So this is called O(n) time complexity, where n is said to represent the number of elements.

Trees and graphs, examples of non-linear data structures, may sometimes cause fastened search times. For example, time complexity in a binary search tree could be as low as O(log n). This is because we split the data with each step involved. Another way to say this is that every time we search, we cut the problem in half.

Common Time Complexities for Data Structures

Time Complexity comparison of most operations between linear and non-linear data structures:

Operation	Array	Linked List	Stack/Queue	Binary Tree	Graph
Search	O(n)	O(n)	O(n)	O(log n)	O(V + E)
Insert	O(1)	O(1)	O(1)	O(log n)	O(1)
Delete	O(n)	O(1)	O(1)	O(log n)	O(E)
Traversal	O(n)	O(n)	O(n)	O(n)	O(V + E)

As demonstrated above, a binary tree is faster than a linear structure, like an array or a linked list, for example, searching or inserting. However, graphs depend solely on the number of nodes (V) and edges (E).

Choosing the Right Data Structure for Your Project

If you are working with something small, such as a very basic task list or contact list, linear structures could be sufficient. They’re easy to implement and quite fine for simple applications.

However, if your data is large or if there are complicated relations between them, then non-linear structures are musts. For instance, one example can be building a social network or a way-finding application where graphs are a good choice for better performance.

A thumb rule is this

Use arrays or linked lists when the dataset is small, and data relations are simple.
Use binary trees when searching and sorting are performed quickly.
Model relationships between data points, like the popularity of particular people in a social network or the transport routes between cities with graphs.

Practical Applications of Linear and Non-Linear Data Structures

Data structures are best suited to do different things. Here is a general overview of where they fit well:

Linear Data Structures

Task Management Apps: An array or a linked list can handle a simple list of tasks, where each task is processed one after the other.

Customer Service Queues: The queue structure suits the application of calls for customer service where one call is taken before the subsequent one

Simple Sorting Algorithms: Sorting an array is quicker for a small set of data than making use of complex structures

Non-Linear Data Structures

Social Networks: Graphs are also implemented in applications, such as Facebook or Instagram, to represent friendships or followers.

Searched on Google: It makes use of binary trees and other non-linear structures that allow huge datasets to be searched in milliseconds.

Navigation: Services like Google Maps model all roads and intersections by calculating the fastest route for somebody as a graph.

Within these applications above, picking the suitable data structure clearly makes a difference in these terms.

Conclusion

Choosing between linear and non-linear data structures depends on the type of data and how it needs to be handled.

There are more linear data structures, like an array and a linked list, that are usable in simple and sequential operations. They are easier to use and access faster in smaller datasets. Non-linear data structures refer to the set of trees and graphs. These are to be used when relationships are complex, thus offering greater flexibility and performance with larger or interconnected datasets.

Knowing the difference between linear and non-linear data structures gives us a chance to optimise both memory usage and time complexity.

Use the appropriate data structure and enhance your application’s performance and scalability significantly.

FAQs

What are the most significant differences between linear and non-linear data structures?

There are two principal differences which can be determined by how data is arranged. Linear data structures store data in a linear sequence, while non-linear structures, either hierarchically or with the help of relations, organise data.

In which scenarios should we use a linear data structure over a non-linear one?

The linear data structures are most applicable for smaller datasets or when the order of the elements matters, such as lists of pending tasks to be done or customer queues.

Are non-linear data structures always better in terms of memory usage compared to a linear structure?

No. That's why we use non-linear data structures: they are more effective in handling complex data, though in small, simple datasets, 'linear' may have less memory usage.

Can a graph be considered both a linear and non-linear data structure?

No, a graph is always non-linear because data is represented in a non-linear sequence form of nodes and edges without any predetermined sequence.

What are the general applications of linear and non-linear data structures used in AI and machine learning?

In AI and machine learning, non-linear structures like trees or graphs are typically applied when decision-making or relational data is present; otherwise, linear structures such as an array would be sufficient if feature storage and input/output management are done.

Updated on September 24, 2024

Link

Upskill with expert articles

View all

Free courses curated for you

Basics of Python

5 Hrs. duration

Beginner level

9 Modules

Certification included

1800+ Learners

View

Essentials of Excel

4 Hrs. duration

Beginner level

12 Modules

Certification included

2200+ Learners

View

Basics of SQL

12 Hrs. duration

Beginner level

12 Modules

Certification included

2600+ Learners

View

Hero Vired is a leading LearnTech company dedicated to offering cutting-edge programs in collaboration with top-tier global institutions. As part of the esteemed Hero Group, we are committed to revolutionizing the skill development landscape in India. Our programs, delivered by industry experts, are designed to empower professionals and students with the skills they need to thrive in today’s competitive job market.

Data Science

Accelerator Program in Business Analytics & Data Science

Integrated Program in Data Science, AI and ML

Accelerator Program in AI and Machine Learning

Advanced Certification Program in Data Science & Analytics

Certification Program in Data Analytics

Technology

Certificate Program in Full Stack Development with Specialization for Web and Mobile

Certificate Program in DevOps and Cloud Engineering

Certificate Program in Application Development

Certificate Program in Cybersecurity Essentials & Risk Assessment

Finance